P-matrix
Encyclopedia
In mathematics
, a -matrix is a complex square matrix with every principal minor
-matrix is a complex square matrix with every principal minor
> 0. A closely related class is that of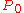 -matrices, which are the closure of the class of
-matrices, which are the closure of the class of  -matrices, with every principal minor
-matrices, with every principal minor  0.
0.
Spectra of
By a theorem of Kellogg, the eigenvalues of 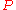 - and
- and 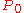 - matrices are bounded away from a wedge about the negative real axis as follows:
- matrices are bounded away from a wedge about the negative real axis as follows:
is a subset of the class of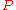 -matrices. More precisely, all matrices that are both
-matrices. More precisely, all matrices that are both 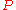 -matrices and Z-matrices are nonsingular
-matrices and Z-matrices are nonsingular  -matrices. The class of sufficient matrices is another generalization of
-matrices. The class of sufficient matrices is another generalization of 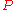 -matrices.
-matrices.
If the Jacobian of a function is a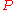 -matrix, then the function is injective on any rectangular region of
-matrix, then the function is injective on any rectangular region of 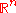 .
.
A related class of interest, particularly with reference to stability, is that of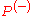 -matrices, sometimes also referred to as
-matrices, sometimes also referred to as  -matrices. A matrix
-matrices. A matrix  is a
is a 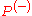 -matrix if and only if
-matrix if and only if 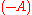 is a
is a 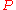 -matrix (similarly for
-matrix (similarly for 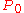 -matrices). Since
-matrices). Since 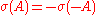 , the eigenvalues of these matrices are bounded away from the positive real axis.
, the eigenvalues of these matrices are bounded away from the positive real axis.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a
 -matrix is a complex square matrix with every principal minor
-matrix is a complex square matrix with every principal minorMinor (linear algebra)
In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns...
> 0. A closely related class is that of
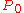 -matrices, which are the closure of the class of
-matrices, which are the closure of the class of 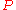 -matrices, with every principal minor
-matrices, with every principal minor  0.
0. Spectra of 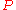 -matrices
-matrices
By a theorem of Kellogg, the eigenvalues of 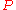 - and
- and 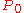 - matrices are bounded away from a wedge about the negative real axis as follows:
- matrices are bounded away from a wedge about the negative real axis as follows:- If
 are the eigenvalues of an
are the eigenvalues of an  -dimensional
-dimensional 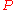 -matrix, then
-matrix, then
- If
 ,
,  ,
, 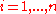 are the eigenvalues of an
are the eigenvalues of an  -dimensional
-dimensional 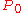 -matrix, then
-matrix, then
Remarks
The class of nonsingular M-matricesM-matrix
In mathematics, especially linear algebra, an M-matrix is a Z-matrix with eigenvalues whose real parts are positive. M-matrices are a subset of the class of P-matrices, and also of the class of inverse-positive matrices In mathematics, especially linear algebra, an M-matrix is a Z-matrix with...
is a subset of the class of
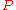 -matrices. More precisely, all matrices that are both
-matrices. More precisely, all matrices that are both 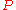 -matrices and Z-matrices are nonsingular
-matrices and Z-matrices are nonsingular  -matrices. The class of sufficient matrices is another generalization of
-matrices. The class of sufficient matrices is another generalization of 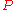 -matrices.
-matrices.If the Jacobian of a function is a
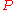 -matrix, then the function is injective on any rectangular region of
-matrix, then the function is injective on any rectangular region of 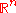 .
.A related class of interest, particularly with reference to stability, is that of
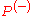 -matrices, sometimes also referred to as
-matrices, sometimes also referred to as  -matrices. A matrix
-matrices. A matrix  is a
is a 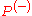 -matrix if and only if
-matrix if and only if 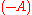 is a
is a 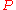 -matrix (similarly for
-matrix (similarly for 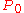 -matrices). Since
-matrices). Since 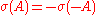 , the eigenvalues of these matrices are bounded away from the positive real axis.
, the eigenvalues of these matrices are bounded away from the positive real axis.