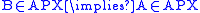PTAS reduction
Encyclopedia
In computational complexity theory
, a PTAS reduction is a reduction
that is often used to perform reductions between solutions to optimization problem
s. It preserves the property that a problem has a polynomial time approximation scheme (PTAS) and is used to define completeness
for certain classes of optimization problem
s such as APX
. Notationally, if there is a PTAS reduction from a problem A to a problem B, we write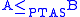 .
.
With ordinary polynomial-time many-one reductions, if we can describe a reduction
from a problem A to a problem B, then any polynomial-time solution for B can be composed with that reduction to obtain a polynomial-time solution for the problem A. Similarly, our goal in defining PTAS reductions is so that given a PTAS reduction from an optimization problem A to a problem B, a PTAS for B can be composed with the reduction to obtain a PTAS for the problem A.
Formally, we define a PTAS reduction from A to B using three polynomial-time computable functions, f, g, and α, with the following properties:
From this definition it is straightforward to show that:
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, a PTAS reduction is a reduction
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
that is often used to perform reductions between solutions to optimization problem
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
s. It preserves the property that a problem has a polynomial time approximation scheme (PTAS) and is used to define completeness
Complete (complexity)
In computational complexity theory, a computational problem is complete for a complexity class if it is, in a formal sense, one of the "hardest" or "most expressive" problems in the complexity class...
for certain classes of optimization problem
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
s such as APX
APX
In complexity theory the class APX is the set of NP optimization problems that allow polynomial-time approximation algorithms with approximation ratio bounded by a constant...
. Notationally, if there is a PTAS reduction from a problem A to a problem B, we write
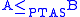 .
.With ordinary polynomial-time many-one reductions, if we can describe a reduction
Reduction
Reduction, reduced, or reduce may refer to:- Chemistry :* Reduction, part of a reduction-oxidation reaction where oxygen is being removed from a compound.** Reduced gas, a gas with a low oxidation number...
from a problem A to a problem B, then any polynomial-time solution for B can be composed with that reduction to obtain a polynomial-time solution for the problem A. Similarly, our goal in defining PTAS reductions is so that given a PTAS reduction from an optimization problem A to a problem B, a PTAS for B can be composed with the reduction to obtain a PTAS for the problem A.
Formally, we define a PTAS reduction from A to B using three polynomial-time computable functions, f, g, and α, with the following properties:
- f maps instances of problem A to instances of problem B.
- g takes an instance x of problem A, an approximate solution to the corresponding problem
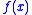 in B, and an error parameter ε and produces an approximate solution to x.
in B, and an error parameter ε and produces an approximate solution to x. - α maps error parameters for solutions to instances of problem A to error parameters for solutions to problem B.
- If the solution y to
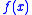 (an instance of problem B) is at most
(an instance of problem B) is at most 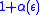 times worse than the optimal solution, then the corresponding solution
times worse than the optimal solution, then the corresponding solution 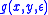 to x (an instance of problem A) is at most
to x (an instance of problem A) is at most  times worse than the optimal solution.
times worse than the optimal solution.
From this definition it is straightforward to show that:
-
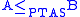 and
and 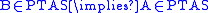
-
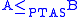 and
and 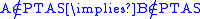
-
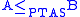 and
and