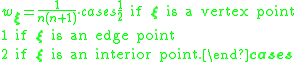Padua points
Encyclopedia
In polynomial interpolation
of two variables
, the Padua points are the first known example (and up to now the only one) of unisolvent
point set (that is, the interpolating polynomial is unique) with minimal growth of their Lebesgue constant
, proven to be O(log2 n)
.
Their name is due to the University of Padua
, where they were originally discovered.
The points are defined in the domain
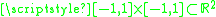. It is possible to use the points with four orientations, obtained with subsequent 90-degree rotations: this way we get four different families of Padua points.
" of a parametric curve, called generating curve, which is slightly different for each of the four families, so that the points for interpolation degree
and family 
can be defined as
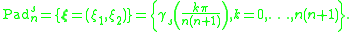
Actually, the Padua points lie exactly on the self-intersections of the curve, and on the intersections of the curve with the boundaries of the square
. The cardinality of the set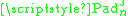 
is 
. Moreover, for each family of Padua points, two points lie on consecutive vertices of the square 
, 
points lie on the edges of the square, and the remaining points lie on the self-intersections of the generating curve inside the square.
The four generating curves are closed parametric curves in the interval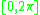
, and are a special case of Lissajous curves
.
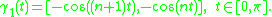
If we sample it as written above, we have:
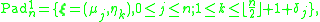
where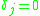
when 
is even or odd but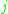 
is even,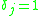 
if
and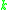 
are both odd
with
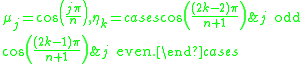
From this follows that the Padua points of first family will have two vertices on the bottom if
is even, or on the left if 
is odd.
which leads to have vertices on the left if
is even and on the bottom if 
is odd.
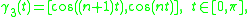
which leads to have vertices on the top if
is even and on the right if 
is odd.
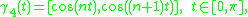
which leads to have vertices on the right if
is even and on the top if 
is odd.
is based on the reproducing kernel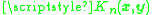
, 
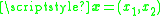and 
, of the space
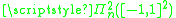equipped with the inner product
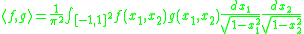
defined by
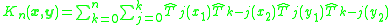
with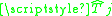
representing the normalized Chebyshev polynomial of degree 
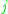(that is, 
, 
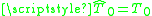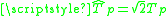where 
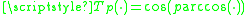is the classical Chebyshev polynomial of first kind of degree 
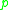). For the four families of Padua points, which we may denote by 
, 
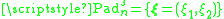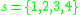, the interpolation formula of order 
of the function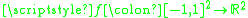 
on the generic target point 
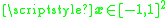is then
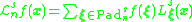
where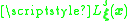
is the fundamental Lagrange polynomial
The weights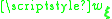
are defined as
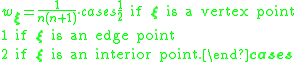
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
of two variables
Multivariate interpolation
In numerical analysis, multivariate interpolation or spatial interpolation is interpolation on functions of more than one variable.The function to be interpolated is known at given points and the interpolation problem consist of yielding values at arbitrary points .-Regular grid:For function...
, the Padua points are the first known example (and up to now the only one) of unisolvent
Unisolvent functions
In mathematics, a collection of n functions ƒ1, ƒ2, ..., ƒn is unisolvent on domain Ω if the vectorsare linearly independent for any choice of n distinct points x1, x2 ... xn in Ω...
point set (that is, the interpolating polynomial is unique) with minimal growth of their Lebesgue constant
Lebesgue constant (interpolation)
In mathematics, the Lebesgue constants give an idea of how good the interpolant of a function is in comparison with the best polynomial approximation of the function...
, proven to be O(log2 n)
.
Their name is due to the University of Padua
University of Padua
The University of Padua is a premier Italian university located in the city of Padua, Italy. The University of Padua was founded in 1222 as a school of law and was one of the most prominent universities in early modern Europe. It is among the earliest universities of the world and the second...
, where they were originally discovered.
The points are defined in the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
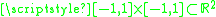. It is possible to use the points with four orientations, obtained with subsequent 90-degree rotations: this way we get four different families of Padua points.The four families
We can see the Padua point as a "samplingSampling (signal processing)
In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of a sound wave to a sequence of samples ....
" of a parametric curve, called generating curve, which is slightly different for each of the four families, so that the points for interpolation degree
and family can be defined as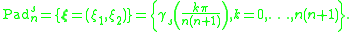Actually, the Padua points lie exactly on the self-intersections of the curve, and on the intersections of the curve with the boundaries of the square
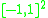. The cardinality of the set 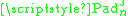is . Moreover, for each family of Padua points, two points lie on consecutive vertices of the square , points lie on the edges of the square, and the remaining points lie on the self-intersections of the generating curve inside the square.The four generating curves are closed parametric curves in the interval
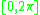, and are a special case of Lissajous curvesLissajous curve
In mathematics, a Lissajous curve , also known as Lissajous figure or Bowditch curve, is the graph of a system of parametric equationswhich describe complex harmonic motion...
.
The first family
The generating curve of Padua points of the first family is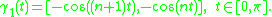If we sample it as written above, we have:
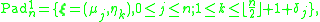
where
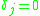when is even or odd but 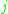is even,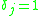 if
and 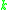are both oddwith
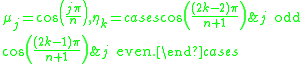
From this follows that the Padua points of first family will have two vertices on the bottom if
is even, or on the left if is odd.The second family
The generating curve of Padua points of the second family iswhich leads to have vertices on the left if
is even and on the bottom if is odd.The third family
The generating curve of Padua points of the third family is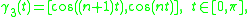which leads to have vertices on the top if
is even and on the right if is odd.The fourth family
The generating curve of Padua points of the fourth family is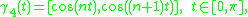which leads to have vertices on the right if
is even and on the top if is odd.The interpolation formula
The explicit representation of their fundamental Lagrange polynomialLagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
is based on the reproducing kernel
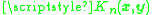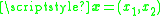, and , of the spaceFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
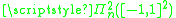equipped with the inner product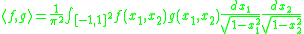defined by
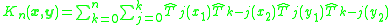
with
representing the normalized Chebyshev polynomial of degree (that is, , 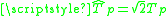where 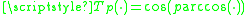is the classical Chebyshev polynomial of first kind of degree 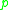). For the four families of Padua points, which we may denote by 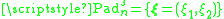, , 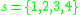the interpolation formula of order of the function 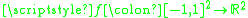on the generic target point 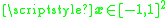is then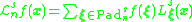where
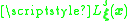is the fundamental Lagrange polynomialThe weights
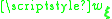are defined as