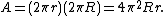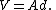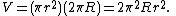In mathematics, Pappus' centroid theorem (also known as the Guldinus theorem, Pappus–Guldinus theorem or Pappus' theorem) is either of two related theorem

Theorem

In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...

s dealing with the surface area

Surface area

Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...

s and volume

Volume

Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....

s of surface

Surface of revolution

A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....

s and solid

Solid of revolution

In mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane....

s of revolution.

The theorem is attributed to Pappus of Alexandria

Pappus of Alexandria

Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...

 and Paul Guldin

Paul Guldin

Paul Guldin was a Swiss Jesuit mathematician and astronomer. He discovered the Guldinus theorem to determine the surface and the volume of a solid of revolution. This theorem is also known as Pappus–Guldinus theorem and Pappus's centroid theorem, attributed to Pappus of Alexandria...

.

The first theorem

The first theorem states that the surface area

Surface area

Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...

 A of a surface of revolution

Surface of revolution

A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....

 generated by rotating a plane curve

Plane curve

In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....

 C about an axis external to C and on the same plane is equal to the product of the arc length

Arc length

Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...

 s of C and the distance d traveled by its geometric centroid

Centroid

In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...

.

For example, the surface area of the torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

 with minor radius

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

 r and major radius R is

The second theorem

The second theorem states that the volume

Volume

Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....

 V of a solid of revolution

Solid of revolution

In mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane....

 generated by rotating a plane figure F about an external axis is equal to the product of the area A of F and the distance d traveled by its geometric centroid.

For example, the volume of the torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

with minor radius r and major radius R is