Parabolic partial differential equation
Encyclopedia
A parabolic partial differential equation is a type of second-order partial differential equation
(PDE), describing a wide family of problems in science including heat diffusion, ocean acoustic propagation
, in physical or mathematical systems with a time variable, and which behave essentially like heat diffusing through a solid.
A partial differential equation of the form
is parabolic if it satisfies the condition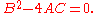
This definition is analogous to the definition of a planar parabola.
A simple example of a parabolic PDE is the one-dimensional heat equation
,
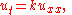
where
is the temperature at time 
and at position 
, and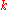 
is a constant. The symbol 
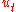signifies the partial derivative
with respect to the time variable
, and similarly 
is the second partial derivative with respect to 
.
This equation says roughly that the temperature at a given time and point will rise or fall at a rate proportional to the difference between the temperature at that point and the average temperature near that point. The quantity
measures how far off the temperature is from satisfying the mean value property of harmonic functions.
A generalization of the heat equation is
where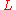
is a second order elliptic operator
(implying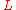
must be positive also; a case where 
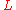is non-positive is described below). Such a system can be hidden in an equation of the form
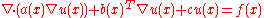
if the matrix-valued function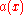
has a kernel
of dimension 1.
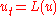is considered to be parabolic if L is a (possibly nonlinear) function of u and its first and second derivatives, with some further conditions on L. With such a nonlinear parabolic differential equation, solutions exist for a short time but may explode in a singularity
in a finite amount of time. Hence, the difficulty is in determining solutions for all time, or more generally studying the singularities that arise. This is in general quite difficult, as in the solution of the Poincaré conjecture via Ricci flow
.
where 
is a positive elliptic operator
. While these problems are no longer necessarily well-posed (solutions may grow unbounded in finite time, or not even exist), they occur when studying the reflection of singularities of solutions to various other PDEs.
This class of equations is closely related to standard hyperbolic equations, which can be seen easily by considering the so-called 'backwards heat equation':
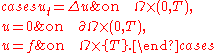
This is essentially the same as the backward hyperbolic equation:
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
(PDE), describing a wide family of problems in science including heat diffusion, ocean acoustic propagation
Underwater acoustics
Underwater acoustics is the study of the propagation of sound in water and the interaction of the mechanical waves that constitute sound with the water and its boundaries. The water may be in the ocean, a lake or a tank. Typical frequencies associated with underwater acoustics are between 10 Hz and...
, in physical or mathematical systems with a time variable, and which behave essentially like heat diffusing through a solid.
A partial differential equation of the form
is parabolic if it satisfies the condition
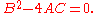
This definition is analogous to the definition of a planar parabola.
A simple example of a parabolic PDE is the one-dimensional heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
,
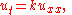
where
is the temperature at time and at position , and 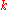is a constant. The symbol 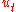signifies the partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
with respect to the time variable
, and similarly is the second partial derivative with respect to .This equation says roughly that the temperature at a given time and point will rise or fall at a rate proportional to the difference between the temperature at that point and the average temperature near that point. The quantity
measures how far off the temperature is from satisfying the mean value property of harmonic functions.A generalization of the heat equation is
where
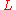is a second order elliptic operatorElliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
(implying
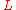must be positive also; a case where 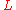is non-positive is described below). Such a system can be hidden in an equation of the form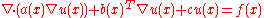if the matrix-valued function
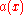has a kernelKernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of dimension 1.
Solution
Under broad assumptions, parabolic PDEs as given above have solutions for all x,y and t>0. An equation of the form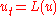 is considered to be parabolic if L is a (possibly nonlinear) function of u and its first and second derivatives, with some further conditions on L. With such a nonlinear parabolic differential equation, solutions exist for a short time but may explode in a singularityMathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
in a finite amount of time. Hence, the difficulty is in determining solutions for all time, or more generally studying the singularities that arise. This is in general quite difficult, as in the solution of the Poincaré conjecture via Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
.
Backward parabolic equation
One may occasionally wish to consider PDEs of the form where is a positive elliptic operatorElliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
. While these problems are no longer necessarily well-posed (solutions may grow unbounded in finite time, or not even exist), they occur when studying the reflection of singularities of solutions to various other PDEs.
This class of equations is closely related to standard hyperbolic equations, which can be seen easily by considering the so-called 'backwards heat equation':
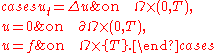
This is essentially the same as the backward hyperbolic equation:
See also
- Hyperbolic partial differential equationHyperbolic partial differential equationIn mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
- Elliptic partial differential equation