
Paris' law
Encyclopedia
Paris' law relates the stress intensity factor
range to sub-critical crack growth under a fatigue
stress regime. As such, it is the most popular fatigue crack growth model used in materials science
and fracture mechanics
. The basic formula reads ,
,
where a is the crack length and N is the number of load cycles. Thus, the term on the left side, known as the crack growth rate, denotes the infinitesimal
crack length growth per increasing number of load cycles. On the right hand side, C and m are material constants, and is the range of the stress intensity factor, i.e., the difference between the stress intensity factor at maximum and minimum loading
is the range of the stress intensity factor, i.e., the difference between the stress intensity factor at maximum and minimum loading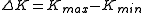 ,
,
where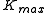 is the maximum stress intensity factor and
is the maximum stress intensity factor and  is the minimum stress intensity factor.
is the minimum stress intensity factor.
relationship between the crack growth rate during cyclic loading and the range of the stress intensity factor, the Paris law can be visualized as a linear graph on a log-log plot, where the x-axis is denoted by the range of the stress intensity factor and the y-axis is denoted by the crack growth rate.
Paris' law can be used to quantify the residual life (in terms of load cycles) of a specimen given a particular crack size. Defining the crack intensity factor as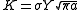 ,
,
where is a uniform tensile stress perpendicular to the crack plane and Y is a dimensionless parameter that depends on the geometry, the range of the stress intensity factor follows as
is a uniform tensile stress perpendicular to the crack plane and Y is a dimensionless parameter that depends on the geometry, the range of the stress intensity factor follows as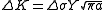 ,
,
where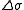 is the range of cyclic stress amplitude. Y takes the value 1 for a center crack in an infinite sheet. The remaining cycles can be found by substituting this equation in the Paris law
is the range of cyclic stress amplitude. Y takes the value 1 for a center crack in an infinite sheet. The remaining cycles can be found by substituting this equation in the Paris law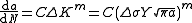 .
.
For relatively short cracks, Y can be assumed as independent of a and the differential equation
can be solved via separation of variables
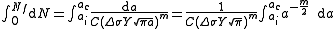
and subsequent integration
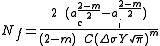 ,
,
where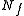 is the remaining number of cycles to fracture,
is the remaining number of cycles to fracture, 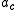 is the critical crack length at which instantaneous fracture will occur, and
is the critical crack length at which instantaneous fracture will occur, and 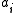 is the initial crack length at which fatigue crack growth starts for the given stress range
is the initial crack length at which fatigue crack growth starts for the given stress range 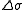 . If Y strongly depends on a, numerical methods might be required to find reasonable solutions.
. If Y strongly depends on a, numerical methods might be required to find reasonable solutions.
For the application to adhesive joints in composites, it is more useful to express the Paris Law in terms of fracture energy rather than stress intensity factors.
Stress Intensity Factor
The stress intensity factor, K, is used in fracture mechanics to predict the stress state near the tip of a crack caused by a remote load or residual stresses. It is a theoretical construct usually applied to a homogeneous, linear elastic material and is useful for providing a failure criterion...
range to sub-critical crack growth under a fatigue
Fatigue (material)
'In materials science, fatigue is the progressive and localized structural damage that occurs when a material is subjected to cyclic loading. The nominal maximum stress values are less than the ultimate tensile stress limit, and may be below the yield stress limit of the material.Fatigue occurs...
stress regime. As such, it is the most popular fatigue crack growth model used in materials science
Materials science
Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...
and fracture mechanics
Fracture mechanics
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.In...
. The basic formula reads
 ,
,where a is the crack length and N is the number of load cycles. Thus, the term on the left side, known as the crack growth rate, denotes the infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
crack length growth per increasing number of load cycles. On the right hand side, C and m are material constants, and
 is the range of the stress intensity factor, i.e., the difference between the stress intensity factor at maximum and minimum loading
is the range of the stress intensity factor, i.e., the difference between the stress intensity factor at maximum and minimum loading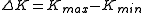 ,
,where
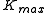 is the maximum stress intensity factor and
is the maximum stress intensity factor and  is the minimum stress intensity factor.
is the minimum stress intensity factor.History and use
The formula was introduced by P.C. Paris in 1961. Being a power lawPower law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
relationship between the crack growth rate during cyclic loading and the range of the stress intensity factor, the Paris law can be visualized as a linear graph on a log-log plot, where the x-axis is denoted by the range of the stress intensity factor and the y-axis is denoted by the crack growth rate.
Paris' law can be used to quantify the residual life (in terms of load cycles) of a specimen given a particular crack size. Defining the crack intensity factor as
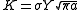 ,
,where
 is a uniform tensile stress perpendicular to the crack plane and Y is a dimensionless parameter that depends on the geometry, the range of the stress intensity factor follows as
is a uniform tensile stress perpendicular to the crack plane and Y is a dimensionless parameter that depends on the geometry, the range of the stress intensity factor follows as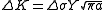 ,
,where
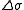 is the range of cyclic stress amplitude. Y takes the value 1 for a center crack in an infinite sheet. The remaining cycles can be found by substituting this equation in the Paris law
is the range of cyclic stress amplitude. Y takes the value 1 for a center crack in an infinite sheet. The remaining cycles can be found by substituting this equation in the Paris law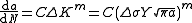 .
.For relatively short cracks, Y can be assumed as independent of a and the differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
can be solved via separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
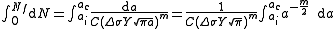
and subsequent integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
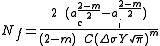 ,
,where
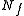 is the remaining number of cycles to fracture,
is the remaining number of cycles to fracture, 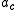 is the critical crack length at which instantaneous fracture will occur, and
is the critical crack length at which instantaneous fracture will occur, and 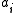 is the initial crack length at which fatigue crack growth starts for the given stress range
is the initial crack length at which fatigue crack growth starts for the given stress range 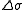 . If Y strongly depends on a, numerical methods might be required to find reasonable solutions.
. If Y strongly depends on a, numerical methods might be required to find reasonable solutions.For the application to adhesive joints in composites, it is more useful to express the Paris Law in terms of fracture energy rather than stress intensity factors.

