
Stress Intensity Factor
Encyclopedia
The stress intensity factor,  , is used in fracture mechanics
, is used in fracture mechanics
to predict the stress state ("stress intensity") near the tip of a crack caused by a remote load
or residual stresses. It is a theoretical construct usually applied to a homogeneous, linear elastic
material and is useful for providing a failure criterion for brittle materials. The concept can also be applied to materials that exhibit small-scale yield
ing at a crack tip.
The magnitude of depends on sample geometry, the size and location of the crack, and the magnitude and the modal distribution of loads on the material.
depends on sample geometry, the size and location of the crack, and the magnitude and the modal distribution of loads on the material.
Linear elastic
theory predicts that the stress distribution (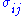 ) near the crack tip, in polar coordinates (
) near the crack tip, in polar coordinates (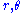 ) with origin at the crack tip, has the form
) with origin at the crack tip, has the form 
where is the stress intensity factor (with units of stress
is the stress intensity factor (with units of stress  length1/2) and
length1/2) and  is a dimensionless quantity that depends on the load and geometry. This relation breaks down very close to the tip (small
is a dimensionless quantity that depends on the load and geometry. This relation breaks down very close to the tip (small  ) because as
) because as  goes to 0, the stress
goes to 0, the stress  goes to
goes to  . Plastic
. Plastic
distortion typically occurs at high stresses and the linear elastic solution is no longer applicable close to the crack tip. However, if the crack-tip plastic zone is small, it can be assumed that the stress distribution near the crack is still given by the above relation.
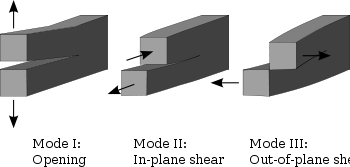 Three linearly independent cracking modes are used in fracture mechanics. These load types are categorized as Mode I, II, or III as shown in the figure. Mode I, shown to the right, is an opening (tensile) mode where the crack surfaces move directly apart. Mode II is a sliding (in-plane shear
Three linearly independent cracking modes are used in fracture mechanics. These load types are categorized as Mode I, II, or III as shown in the figure. Mode I, shown to the right, is an opening (tensile) mode where the crack surfaces move directly apart. Mode II is a sliding (in-plane shear
) mode where the crack surfaces slide over one another in a direction perpendicular to the leading edge of the crack. Mode III is a tearing (antiplane shear
) mode where the crack surfaces move relative to one another and parallel to the leading edge of the crack. Mode I is the most common load type encountered in engineering design.
Different subscripts are used to designate the stress intensity factor for the three different modes. The stress intensity factor for mode I is designated and applied to the crack opening mode. The mode II stress intensity factor,
and applied to the crack opening mode. The mode II stress intensity factor, 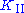 , applies to the crack sliding mode and the mode III stress intensity factor,
, applies to the crack sliding mode and the mode III stress intensity factor,  , applies to the tearing mode. These factors are formally defined as
, applies to the tearing mode. These factors are formally defined as 
( ) for a crack under mode I loading is related to the stress intensity factor by
) for a crack under mode I loading is related to the stress intensity factor by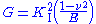
where is the Young's modulus
is the Young's modulus
and is the Poisson's ratio
is the Poisson's ratio
of the material. The material is assumed to be an isotropic, homogeneous, and linear elastic. Plane strain has been assumed and the crack has been assumed to extend along the direction of the initial crack. For plane stress conditions, the above relation simplifies to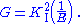
For pure mode II loading, we have similar relations
For pure mode III loading,
where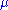 is the shear modulus. For general loading in plane strain, the relationship between the strain energy and the stress intensity factors for the three modes is
is the shear modulus. For general loading in plane strain, the relationship between the strain energy and the stress intensity factors for the three modes is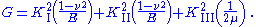
A similar relation is obtained for plane stress by adding the contributions for the three modes.
The above relations can also be used to connect the J integral
to the stress intensity factor because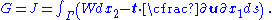
 , is a parameter that amplifies the magnitude of the applied stress that includes the geometrical parameter
, is a parameter that amplifies the magnitude of the applied stress that includes the geometrical parameter  (load type). Stress intensity in any mode situation is directly proportional to the applied load on the material. If a very sharp crack can be made in a material, the minimum value of
(load type). Stress intensity in any mode situation is directly proportional to the applied load on the material. If a very sharp crack can be made in a material, the minimum value of  can be empirically determined, which is the critical value of stress intensity required to propagate the crack. This critical value determined for mode I loading in plane strain is referred to as the critical fracture toughness (
can be empirically determined, which is the critical value of stress intensity required to propagate the crack. This critical value determined for mode I loading in plane strain is referred to as the critical fracture toughness ( ) of the material.
) of the material.  has units of stress times the root of a distance. The units of
has units of stress times the root of a distance. The units of  imply that the fracture stress of the material must be reached over some critical distance in order for
imply that the fracture stress of the material must be reached over some critical distance in order for  to be reached and crack propagation to occur. The Mode I critical stress intensity factor,
to be reached and crack propagation to occur. The Mode I critical stress intensity factor,  , is the most often used engineering design parameter in fracture mechanics and hence must be understood if we are to design fracture tolerant materials used in bridges, buildings, aircraft, or even bells. Polishing cannot detect a crack. Typically, if a crack can be seen it is very close to the critical stress state predicted by the stress intensity factor.
, is the most often used engineering design parameter in fracture mechanics and hence must be understood if we are to design fracture tolerant materials used in bridges, buildings, aircraft, or even bells. Polishing cannot detect a crack. Typically, if a crack can be seen it is very close to the critical stress state predicted by the stress intensity factor.
that relates the critical stress intensity factor (or fracture toughness) to the stress intensity factors for the three modes. This failure criterion is written as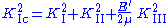
where is the mode I fracture toughness,
is the mode I fracture toughness, 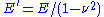 for plane strain and
for plane strain and  for plane stress. The critical stress intensity factor for plane stress is often written as
for plane stress. The critical stress intensity factor for plane stress is often written as  .
.
 , is used in fracture mechanics
, is used in fracture mechanicsFracture mechanics
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.In...
to predict the stress state ("stress intensity") near the tip of a crack caused by a remote load
Structural load
Structural loads or actions are forces, deformations or accelerations applied to a structure or its components.Loads cause stresses, deformations and displacements in structures. Assessment of their effects is carried out by the methods of structural analysis...
or residual stresses. It is a theoretical construct usually applied to a homogeneous, linear elastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
material and is useful for providing a failure criterion for brittle materials. The concept can also be applied to materials that exhibit small-scale yield
Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
ing at a crack tip.
The magnitude of
 depends on sample geometry, the size and location of the crack, and the magnitude and the modal distribution of loads on the material.
depends on sample geometry, the size and location of the crack, and the magnitude and the modal distribution of loads on the material.Linear elastic
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
theory predicts that the stress distribution (
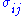 ) near the crack tip, in polar coordinates (
) near the crack tip, in polar coordinates (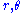 ) with origin at the crack tip, has the form
) with origin at the crack tip, has the form 
where
 is the stress intensity factor (with units of stress
is the stress intensity factor (with units of stress  length1/2) and
length1/2) and  is a dimensionless quantity that depends on the load and geometry. This relation breaks down very close to the tip (small
is a dimensionless quantity that depends on the load and geometry. This relation breaks down very close to the tip (small  ) because as
) because as  goes to 0, the stress
goes to 0, the stress  goes to
goes to  . Plastic
. PlasticPlasticity (physics)
In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
distortion typically occurs at high stresses and the linear elastic solution is no longer applicable close to the crack tip. However, if the crack-tip plastic zone is small, it can be assumed that the stress distribution near the crack is still given by the above relation.
Stress intensity factors for various modes

Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
) mode where the crack surfaces slide over one another in a direction perpendicular to the leading edge of the crack. Mode III is a tearing (antiplane shear
Antiplane shear
Antiplane shear or antiplane strain is a special state of strain in a body. This state of strain is achieved when the displacements in the body are zero in the plane of interest but nonzero in the direction perpendicular to the plane...
) mode where the crack surfaces move relative to one another and parallel to the leading edge of the crack. Mode I is the most common load type encountered in engineering design.
Different subscripts are used to designate the stress intensity factor for the three different modes. The stress intensity factor for mode I is designated
 and applied to the crack opening mode. The mode II stress intensity factor,
and applied to the crack opening mode. The mode II stress intensity factor, 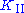 , applies to the crack sliding mode and the mode III stress intensity factor,
, applies to the crack sliding mode and the mode III stress intensity factor,  , applies to the tearing mode. These factors are formally defined as
, applies to the tearing mode. These factors are formally defined as 
Relationship to energy release rate and J-integral
The strain energy release rateStrain energy release rate
Strain energy release rate is the energy dissipated during fracture per unit of newly created fracture surface area. This quantity is central to fracture mechanics because the energy that must be supplied to a crack tip for it to grow must be balanced by the amount of energy dissipated due to the...
(
 ) for a crack under mode I loading is related to the stress intensity factor by
) for a crack under mode I loading is related to the stress intensity factor by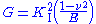
where
 is the Young's modulus
is the Young's modulusYoung's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
and
 is the Poisson's ratio
is the Poisson's ratioPoisson's ratio
Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
of the material. The material is assumed to be an isotropic, homogeneous, and linear elastic. Plane strain has been assumed and the crack has been assumed to extend along the direction of the initial crack. For plane stress conditions, the above relation simplifies to
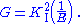
For pure mode II loading, we have similar relations

For pure mode III loading,

where
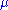 is the shear modulus. For general loading in plane strain, the relationship between the strain energy and the stress intensity factors for the three modes is
is the shear modulus. For general loading in plane strain, the relationship between the strain energy and the stress intensity factors for the three modes is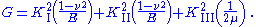
A similar relation is obtained for plane stress by adding the contributions for the three modes.
The above relations can also be used to connect the J integral
J integral
The J-integral represents a way to calculate the strain energy release rate, or work per unit fracture surface area, in a material. The theoretical concept of J-integral was developed in 1967 by Cherepanov and in 1968 by Jim Rice independently, who showed that an energetic contour path integral ...
to the stress intensity factor because
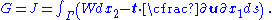
Critical stress intensity factor
The stress intensity factor, , is a parameter that amplifies the magnitude of the applied stress that includes the geometrical parameter
, is a parameter that amplifies the magnitude of the applied stress that includes the geometrical parameter  (load type). Stress intensity in any mode situation is directly proportional to the applied load on the material. If a very sharp crack can be made in a material, the minimum value of
(load type). Stress intensity in any mode situation is directly proportional to the applied load on the material. If a very sharp crack can be made in a material, the minimum value of  can be empirically determined, which is the critical value of stress intensity required to propagate the crack. This critical value determined for mode I loading in plane strain is referred to as the critical fracture toughness (
can be empirically determined, which is the critical value of stress intensity required to propagate the crack. This critical value determined for mode I loading in plane strain is referred to as the critical fracture toughness ( ) of the material.
) of the material.  has units of stress times the root of a distance. The units of
has units of stress times the root of a distance. The units of  imply that the fracture stress of the material must be reached over some critical distance in order for
imply that the fracture stress of the material must be reached over some critical distance in order for  to be reached and crack propagation to occur. The Mode I critical stress intensity factor,
to be reached and crack propagation to occur. The Mode I critical stress intensity factor,  , is the most often used engineering design parameter in fracture mechanics and hence must be understood if we are to design fracture tolerant materials used in bridges, buildings, aircraft, or even bells. Polishing cannot detect a crack. Typically, if a crack can be seen it is very close to the critical stress state predicted by the stress intensity factor.
, is the most often used engineering design parameter in fracture mechanics and hence must be understood if we are to design fracture tolerant materials used in bridges, buildings, aircraft, or even bells. Polishing cannot detect a crack. Typically, if a crack can be seen it is very close to the critical stress state predicted by the stress intensity factor.G–criterion
The G-criterion is a fracture criterionFailure theory (material)
Failure theory is the science of predicting the conditions under which solid materials fail under the action of external loads. The failure of a material is usually classified into brittle failure or ductile failure . Depending on the conditions most materials can fail in a brittle or ductile...
that relates the critical stress intensity factor (or fracture toughness) to the stress intensity factors for the three modes. This failure criterion is written as
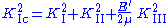
where
 is the mode I fracture toughness,
is the mode I fracture toughness, 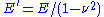 for plane strain and
for plane strain and  for plane stress. The critical stress intensity factor for plane stress is often written as
for plane stress. The critical stress intensity factor for plane stress is often written as  .
.Examples of stress intensity factors
| Uniform uniaxial stress The stress intensity factor for a through crack of length 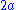 , at right angles, in an infinite plane, to a uniform stress field , at right angles, in an infinite plane, to a uniform stress field  is is  If the crack is located centrally in a finite plate of width  and height and height  , an approximate relation for the stress intensity factor is , an approximate relation for the stress intensity factor is  If the crack is not located centrally along the width, i.e.,  , the stress intensity factor at location A has the form , the stress intensity factor at location A has the form where the factors 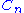 can be found in tabulated form for various values of can be found in tabulated form for various values of 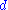 . A similar expression can be found for tip B of the crack. . A similar expression can be found for tip B of the crack. |
|
| Edge crack in a plate under uniaxial stress For a plate of dimensions  containing an edge crack of length containing an edge crack of length  , if the dimensions , if the dimensionsof the plate are such that 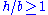 and and  , the stress intensity factor at the , the stress intensity factor at thecrack tip under an uniaxial stress  is is For the situation where 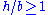 and and  , the stress intensity factor can be approximated , the stress intensity factor can be approximatedby 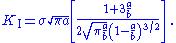 Specimens of this configuration are commonly used in fracture toughness Fracture toughness In materials science, fracture toughness is a property which describes the ability of a material containing a crack to resist fracture, and is one of the most important properties of any material for virtually all design applications. The fracture toughness of a material is determined from the... testing.. |
|
| Slanted crack in a biaxial stress field For a slanted crack of length  in a biaxial stress field with stress in a biaxial stress field with stress  in the in the 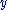 -direction and -direction and  in the in the  -direction, the stress intensity factors are -direction, the stress intensity factors are  where  is the angle made by the crack with the is the angle made by the crack with the  -axis. -axis. |
|
| Penny-shaped crack in an infinite domain The stress intensity factor at the tip of a penny-shaped crack of radius  in an infinite domain under uniaxial tension in an infinite domain under uniaxial tension  is is  |
|
| Crack in a plate under point in-plane force Consider a plate with dimensions 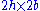 containing a crack of length containing a crack of length 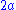 . A point force with components . A point force with components 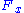 and and 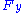 is applied at the point ( is applied at the point ( ) of the plate. ) of the plate.For the situation where the plate is large compared to the size of the crack and the location of the force is relatively close to the crack, i.e.,  , ,  , ,  , ,  , the plate can be considered infinite. In that case, for the stress intensity factors for , the plate can be considered infinite. In that case, for the stress intensity factors for  at crack tip B ( at crack tip B ( ) are ) are  where  with 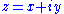 , , 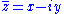 , ,  for plane strain, for plane strain, 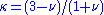 for plane stress, and for plane stress, and  is the Poisson's ratio is the Poisson's ratioPoisson's ratio Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain .... . The stress intensity factors for 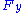 at tip B are at tip B are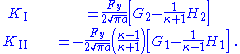 The stress intensity factors at the tip A (  ) can be determined from the above relations. For the load ) can be determined from the above relations. For the load  at location at location  , , Similarly for the load  , ,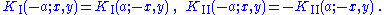 |
|
| Loaded crack in a plate If the crack is loaded by a point force  located at located at  and and  , the stress intensity factors at point B are , the stress intensity factors at point B are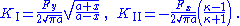 If the force is distributed uniformly between 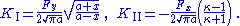 , then the stress intensity factor at tip B is , then the stress intensity factor at tip B is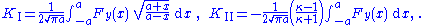 |
Stress intensity factors for fracture toughness tests
| Compact tension specimen The stress intensity factor at the crack tip of a compact tension specimen Compact tension specimen A compact tension specimen is a notched sample and is a standard specimen in accordance with ASTM and ISO standards. The purpose of using a notched sample is to create a fatigue crack by cycling the sample to maximum and minimum loads... is  where  is the applied load, is the applied load, 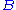 is the thickness of the specimen, is the thickness of the specimen,  is the crack length, and is the crack length, and is the width of the specimen. is the width of the specimen. |
|
| Single edge notch bending specimen The stress intensity factor at the crack tip of a single edge notch bending specimen Three point flexural test The three point bending flexural test provides values for the modulus of elasticityin bending E_f, flexural stress \sigma_f, flexural strain \epsilon_f and the flexural stress-strain response of the material. The main advantage of a three point flexural test is the ease of the specimen preparation... is 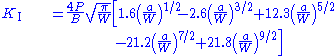 where  is the applied load, is the applied load,  is the thickness of the specimen, is the thickness of the specimen,  is the crack length, and is the crack length, and is the width of the specimen. is the width of the specimen. |
See also
- Fracture mechanicsFracture mechanicsFracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.In...
- Fracture toughnessFracture toughnessIn materials science, fracture toughness is a property which describes the ability of a material containing a crack to resist fracture, and is one of the most important properties of any material for virtually all design applications. The fracture toughness of a material is determined from the...
- Strain energy release rateStrain energy release rateStrain energy release rate is the energy dissipated during fracture per unit of newly created fracture surface area. This quantity is central to fracture mechanics because the energy that must be supplied to a crack tip for it to grow must be balanced by the amount of energy dissipated due to the...
- J integralJ integralThe J-integral represents a way to calculate the strain energy release rate, or work per unit fracture surface area, in a material. The theoretical concept of J-integral was developed in 1967 by Cherepanov and in 1968 by Jim Rice independently, who showed that an energetic contour path integral ...
- Failure theory (material)Failure theory (material)Failure theory is the science of predicting the conditions under which solid materials fail under the action of external loads. The failure of a material is usually classified into brittle failure or ductile failure . Depending on the conditions most materials can fail in a brittle or ductile...

