
J integral
Encyclopedia
The J-integral
represents a way to calculate the strain energy release rate
, or work (energy
) per unit fracture surface area, in a material. The theoretical concept of J-integral was developed in 1967 by Cherepanov and in 1968 by Jim Rice independently, who showed that an energetic contour path integral (called J) was independent of the path around a crack
.
Later, experimental methods were developed, which allowed measurement of critical fracture properties using laboratory-scale specimens for materials in which sample sizes are too small and for which the assumptions of Linear Elastic Fracture Mechanics
(LEFM) do not hold, and to infer a critical value of fracture energy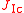 . The quantity
. The quantity 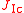 defines the point at which large-scale plastic
defines the point at which large-scale plastic
yielding during propagation takes place under mode one loading.
The J-integral is equal to the strain energy release rate
for a crack in a body subjected to monotonic loading. This is true, under quasistatic conditions, both for linear elastic
materials and for materials that experience small-scale yield
ing at the crack tip.
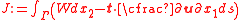
where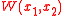 is the strain energy density,
is the strain energy density, 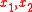 are the coordinate directions,
are the coordinate directions, 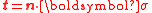 is the surface traction
is the surface traction
vector, is the normal to the curve
is the normal to the curve  ,
,  is the Cauchy stress
is the Cauchy stress
tensor, and is the displacement vector. The strain energy density is given by
is the displacement vector. The strain energy density is given by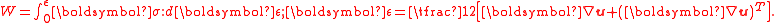
The J-Integral around a crack tip is frequently expressed in a more general form (and in index notation
) as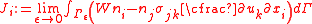
where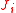 is the component of the J-integral for crack opening in the
is the component of the J-integral for crack opening in the 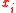 direction and
direction and  is a small region around the crack tip.
is a small region around the crack tip.
Using Green's theorem
we can show that this integral is zero when the boundary is closed and encloses a region that contains no singularities
is closed and encloses a region that contains no singularities
and is simply connected. If the faces of the crack do not have any surface tractions on them then the J-integral is also path independent.
Rice also showed that the value of the J-integral represents the energy release rate for planar crack growth.
The J-integral was developed because of the difficulties involved in computing the stress close to a crack in a nonlinear elastic
or elastic-plastic
material. Rice showed that if monotonic loading was assumed (without any plastic unloading) then the J-integral could be used to compute the energy release rate of plastic materials too.
if the crack extends straight ahead with respect to its original orientation.
For plane strain, under Mode I
loading conditions, this relation is
where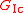 is the critical strain energy release rate,
is the critical strain energy release rate, 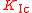 is the fracture toughness in Mode I loading,
is the fracture toughness in Mode I loading,  is the Poisson's ratio, and E is the Young's modulus
is the Poisson's ratio, and E is the Young's modulus
of the material.
For Mode II
loading, the relation between the J-integral and the mode II fracture toughness ( ) is
) is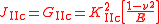
For Mode III
loading, the relation is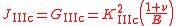
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
represents a way to calculate the strain energy release rate
Strain energy release rate
Strain energy release rate is the energy dissipated during fracture per unit of newly created fracture surface area. This quantity is central to fracture mechanics because the energy that must be supplied to a crack tip for it to grow must be balanced by the amount of energy dissipated due to the...
, or work (energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
) per unit fracture surface area, in a material. The theoretical concept of J-integral was developed in 1967 by Cherepanov and in 1968 by Jim Rice independently, who showed that an energetic contour path integral (called J) was independent of the path around a crack
Crack
Crack may refer to:* Crack cocaine, the freebase form of cocaine that can be smoked* Crack, a fracture or discontinuation in a bodyCrack may also refer to:-Music:* Crack , an album by Z-RO* Cracks , an album by Nabiha...
.
Later, experimental methods were developed, which allowed measurement of critical fracture properties using laboratory-scale specimens for materials in which sample sizes are too small and for which the assumptions of Linear Elastic Fracture Mechanics
Fracture mechanics
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.In...
(LEFM) do not hold, and to infer a critical value of fracture energy
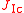 . The quantity
. The quantity 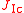 defines the point at which large-scale plastic
defines the point at which large-scale plasticPlasticity (physics)
In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
yielding during propagation takes place under mode one loading.
The J-integral is equal to the strain energy release rate
Strain energy release rate
Strain energy release rate is the energy dissipated during fracture per unit of newly created fracture surface area. This quantity is central to fracture mechanics because the energy that must be supplied to a crack tip for it to grow must be balanced by the amount of energy dissipated due to the...
for a crack in a body subjected to monotonic loading. This is true, under quasistatic conditions, both for linear elastic
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
materials and for materials that experience small-scale yield
Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
ing at the crack tip.
Two-dimensional J-integral
The two-dimensional J-integral was originally defined as (see Figure 1 for an illustration)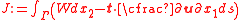
where
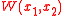 is the strain energy density,
is the strain energy density, 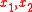 are the coordinate directions,
are the coordinate directions, 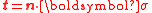 is the surface traction
is the surface tractionStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
vector,
 is the normal to the curve
is the normal to the curve  ,
,  is the Cauchy stress
is the Cauchy stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
tensor, and
 is the displacement vector. The strain energy density is given by
is the displacement vector. The strain energy density is given by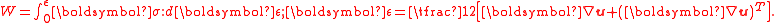
The J-Integral around a crack tip is frequently expressed in a more general form (and in index notation
Einstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
) as
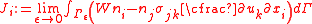
where
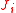 is the component of the J-integral for crack opening in the
is the component of the J-integral for crack opening in the 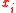 direction and
direction and  is a small region around the crack tip.
is a small region around the crack tip.Using Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
we can show that this integral is zero when the boundary
 is closed and encloses a region that contains no singularities
is closed and encloses a region that contains no singularitiesMathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
and is simply connected. If the faces of the crack do not have any surface tractions on them then the J-integral is also path independent.
Rice also showed that the value of the J-integral represents the energy release rate for planar crack growth.
The J-integral was developed because of the difficulties involved in computing the stress close to a crack in a nonlinear elastic
Elasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
or elastic-plastic
Plasticity (physics)
In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
material. Rice showed that if monotonic loading was assumed (without any plastic unloading) then the J-integral could be used to compute the energy release rate of plastic materials too.
| Proof that the J-integral is zero over a closed path |
|---|
To show the path independence of the J-integral, we first have to show that the value of  is zero over a closed contour in a simply connected domain. Let us just consider the expression for is zero over a closed contour in a simply connected domain. Let us just consider the expression for 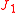 which is which is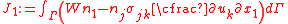 We can write this as  From Green's theorem Green's theorem In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C... (or the two-dimensional divergence theorem Divergence theorem In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem... ) we have 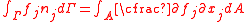 Using this result we can express 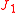 as as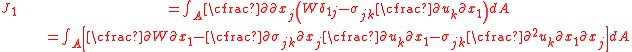 where  is the area enclosed by the contour is the area enclosed by the contour  . Now, if there are no body forces present, equilibrium (conservation of linear momentum) requires that . Now, if there are no body forces present, equilibrium (conservation of linear momentum) requires that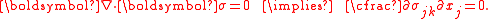 Also, 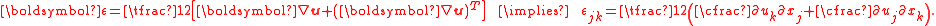 Therefore,  From the balance of angular momentum we have  . Hence, . Hence,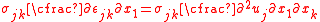 The J-integral may then be written as  Now, for an elastic material the stress can be derived from the stored energy function  using using Then, using the chain rule Chain rule In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the... of differentiation, 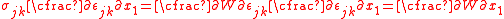 Therefore we have 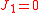 for a closed contour enclosing a simply connected region without any stress singularities. for a closed contour enclosing a simply connected region without any stress singularities. |
| Proof that the J-integral is path-independent |
|---|
Consider the contour  . Since this contour is closed and encloses a simply connected region, the J-integral around the contour is zero, i.e. . Since this contour is closed and encloses a simply connected region, the J-integral around the contour is zero, i.e. assuming that counterclockwise integrals around the crack tip have positive sign. Now, since the crack surfaces are parallel to the 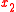 axis, the normal component axis, the normal component 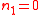 on these surfaces. Also, since the crack surfaces are traction free, on these surfaces. Also, since the crack surfaces are traction free,  . Therefore, . Therefore,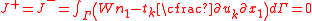 Therefore,  and the J-integral is path independent. |
J-integral and fracture toughness
For isotropic, perfectly brittle, linear elastic materials, the J-integral can be directly related to the fracture toughnessFracture toughness
In materials science, fracture toughness is a property which describes the ability of a material containing a crack to resist fracture, and is one of the most important properties of any material for virtually all design applications. The fracture toughness of a material is determined from the...
if the crack extends straight ahead with respect to its original orientation.
For plane strain, under Mode I
Fracture mechanics
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.In...
loading conditions, this relation is

where
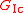 is the critical strain energy release rate,
is the critical strain energy release rate, 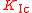 is the fracture toughness in Mode I loading,
is the fracture toughness in Mode I loading,  is the Poisson's ratio, and E is the Young's modulus
is the Poisson's ratio, and E is the Young's modulusYoung's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
of the material.
For Mode II
Fracture mechanics
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.In...
loading, the relation between the J-integral and the mode II fracture toughness (
 ) is
) is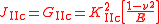
For Mode III
Fracture mechanics
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.In...
loading, the relation is
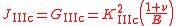
See also
- Fracture toughnessFracture toughnessIn materials science, fracture toughness is a property which describes the ability of a material containing a crack to resist fracture, and is one of the most important properties of any material for virtually all design applications. The fracture toughness of a material is determined from the...
- ToughnessToughnessIn materials science and metallurgy, toughness is the ability of a material to absorb energy and plastically deform without fracturing; Material toughness is defined as the amount of energy per volume that a material can absorb before rupturing...
- Fracture mechanicsFracture mechanicsFracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.In...
- Stress intensity factorStress Intensity FactorThe stress intensity factor, K, is used in fracture mechanics to predict the stress state near the tip of a crack caused by a remote load or residual stresses. It is a theoretical construct usually applied to a homogeneous, linear elastic material and is useful for providing a failure criterion...
External links
- J. R. Rice, "A Path Independent Integral and the Approximate Analysis of Strain Concentration by Notches and Cracks", Journal of Applied Mechanics, 35, 1968, pp. 379-386.
- Van Vliet, Krystyn J. (2006); "3.032 Mechanical Behavior of Materials", http://www.stellar.mit.edu/S/course/3/fa06/3.032/index.html
- Fracture Mechanics Notes by Prof. Alan Zehnder (from Cornell University)
- Nonlinear Fracture Mechanics Notes by Prof. John Hutchinson (from Harvard University)
- Notes on Fracture of Thin Films and Multilayers by Prof. John Hutchinson (from Harvard University)
- Mixed mode cracking in layered materials by Profs. John Hutchinson and Zhigang Suo (from Harvard University)
- Fracture Mechanics by Prof. Piet Schreurs (from TU Eindhoven, Netherlands)
- Introduction to Fracture Mechanics by Dr. C. H. Wang (DSTO - Australia)
- Fracture mechanics course notes by Prof. Rui Huang (from Univ. of Texas at Austin)

