In materials science

Materials science

Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...

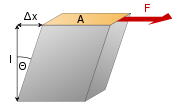
, shear modulus or modulus of rigidity, denoted by G, or sometimes S or μ, is defined as the ratio of shear stress

Shear stress

A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...

 to the shear strain:

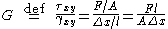
where 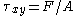= shear stress; 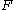is the force which acts 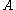is the area on which the force acts

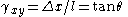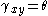
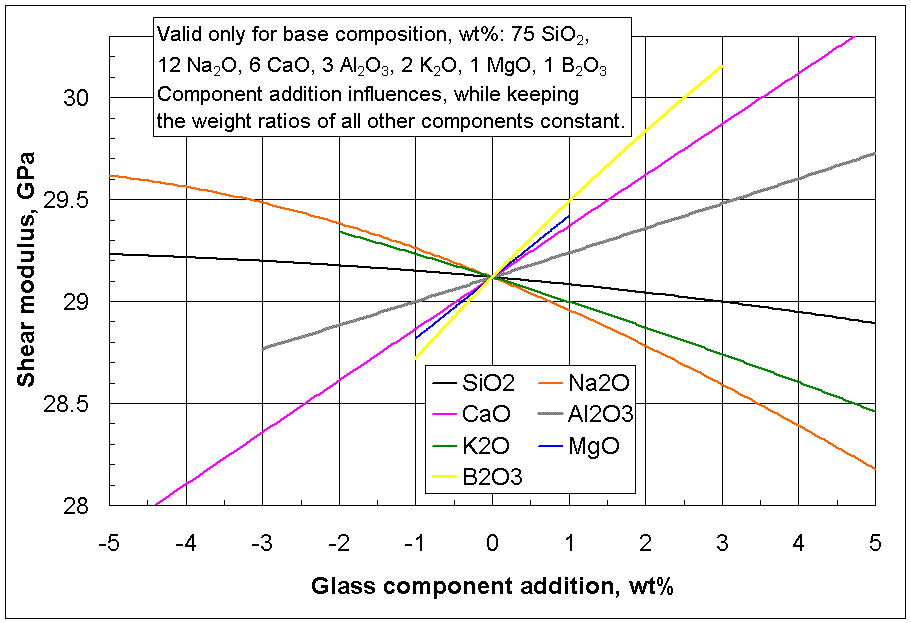
in engineering, = shear strain. Elsewhere, 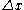is the transverse displacement 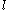is the initial length

Shear modulus is usually expressed in gigapascal

Pascal (unit)

The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...

s (GPa) or in thousands of pounds per square inch (kpsi).

The shear modulus is always positive.

Explanation

Material	Typical values for shear modulus (GPa) (at room temperature)
Diamond Diamond In mineralogy, diamond is an allotrope of carbon, where the carbon atoms are arranged in a variation of the face-centered cubic crystal structure called a diamond lattice. Diamond is less stable than graphite, but the conversion rate from diamond to graphite is negligible at ambient conditions...	478.
Steel Steel Steel is an alloy that consists mostly of iron and has a carbon content between 0.2% and 2.1% by weight, depending on the grade. Carbon is the most common alloying material for iron, but various other alloying elements are used, such as manganese, chromium, vanadium, and tungsten...	79.3
Copper Copper Copper is a chemical element with the symbol Cu and atomic number 29. It is a ductile metal with very high thermal and electrical conductivity. Pure copper is soft and malleable; an exposed surface has a reddish-orange tarnish...	44.7
Titanium Titanium Titanium is a chemical element with the symbol Ti and atomic number 22. It has a low density and is a strong, lustrous, corrosion-resistant transition metal with a silver color....	41.4
Glass Glass Glass is an amorphous solid material. Glasses are typically brittle and optically transparent.The most familiar type of glass, used for centuries in windows and drinking vessels, is soda-lime glass, composed of about 75% silica plus Na2O, CaO, and several minor additives...	26.2
Aluminium Aluminium Aluminium or aluminum is a silvery white member of the boron group of chemical elements. It has the symbol Al, and its atomic number is 13. It is not soluble in water under normal circumstances....	25.5
Polyethylene Polyethylene Polyethylene or polythene is the most widely used plastic, with an annual production of approximately 80 million metric tons...	0.117
Rubber Rubber Natural rubber, also called India rubber or caoutchouc, is an elastomer that was originally derived from latex, a milky colloid produced by some plants. The plants would be ‘tapped’, that is, an incision made into the bark of the tree and the sticky, milk colored latex sap collected and refined...	0.0006

The shear modulus is one of several quantities for measuring the stiffness of materials. All of them arise in the generalized Hooke's law

Hooke's law

In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...

:

• Young's modulus
  Young's modulus
  Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
  
   describes the material's response to linear strain (like pulling on the ends of a wire),
• the bulk modulus
  Bulk modulus
  The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
  
   describes the material's response to uniform pressure
  Pressure
  Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
  
  , and
• the shear modulus describes the material's response to shearing strains.

The shear modulus is concerned with the deformation of a solid when it experiences a force parallel to one of its surfaces while its opposite face experiences an opposing force (such as friction). In the case of an object that's shaped like a rectangular prism, it will deform into a parallelepiped

Parallelepiped

In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...

. Anisotropic materials such as wood

Wood

Wood is a hard, fibrous tissue found in many trees. It has been used for hundreds of thousands of years for both fuel and as a construction material. It is an organic material, a natural composite of cellulose fibers embedded in a matrix of lignin which resists compression...

 and paper

Paper

Paper is a thin material mainly used for writing upon, printing upon, drawing or for packaging. It is produced by pressing together moist fibers, typically cellulose pulp derived from wood, rags or grasses, and drying them into flexible sheets....

 exhibit differing material response to stress or strain when tested in different directions. In this case, when the deformation is small enough so that the deformation is linear, the elastic moduli, including the shear modulus, will then be a tensor, rather than a single scalar value.

Waves

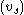In homogeneous and isotropic solids, there are two kinds of waves, pressure waves and shear waves. The velocity of a shear wave, is controlled by the shear modulus,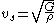
where

G is the shear modulus 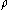is the solid's density

Density

The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...

.

Shear modulus of metals

The shear modulus of metals measures the resistance to glide over atomic planes in crystals of the metal. In polycrystalline metals there are also grain boundary factors that have to be considered. In metal alloys, the shear modulus is observed to be higher than in pure metals due to the presence of additional sources of resistance to glide.

The shear modulus of metals is usually observed to decrease with increasing temperature. At high pressures, the shear modulus also appears to increase with the applied pressure. Correlations between the melting temperature, vacancy formation energy, and the shear modulus have been observed in many metals.

Several models exist that attempt to predict the shear modulus of metals (and possibly that of alloys). Shear modulus models that have been used in plastic flow computations include:

1. the MTS shear modulus model developed by and used in conjunction with the Mechanical Threshold Stress (MTS) plastic flow stress model.
2. the Steinberg-Cochran-Guinan (SCG) shear modulus model developed by and used in conjunction with the Steinberg-Cochran-Guinan-Lund (SCGL) flow stress model.
3. the Nadal and LePoac (NP) shear modulus model that uses Lindemann theory to determine the temperature dependence and the SCG model for pressure dependence of the shear modulus.

MTS shear modulus model

The MTS shear modulus model has the form: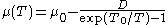


where µ₀ is the shear modulus at 0 K, and D and T₀ are material constants.

SCG shear modulus model

The Steinberg-Cochran-Guinan (SCG) shear modulus model is pressure dependent and has the form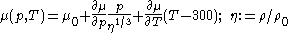
where, µ₀ is the shear modulus at the reference state (T = 300 K, p = 0, η = 1), p is the pressure, and T is the temperature.

NP shear modulus model

The Nadal-Le Poac (NP) shear modulus model is a modified version of the SCG model. The empirical temperature dependence of the shear modulus in the SCG model is replaced with an equation based on Lindemann melting theory. The NP shear modulus model has the form: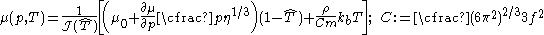


where


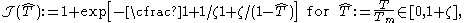
and µ₀ is the shear modulus at 0 K and ambient pressure, ζ is a material parameter, k_b is the Boltzmann constant, m is the atomic mass

Atomic mass

The atomic mass is the mass of a specific isotope, most often expressed in unified atomic mass units. The atomic mass is the total mass of protons, neutrons and electrons in a single atom....

, and f is the Lindemann constant.