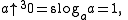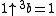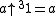Pentation
Encyclopedia
Pentation is the operation of repeated tetration
, just as tetration
is the operation of repeated exponentation and is a hyperoperation
. It is non-commutative, and therefore has two inverse functions, which might be named the penta-root and the penta-logarithm (analogous to the two inverse functions for exponentiation: nth root
function and logarithm
). Pentation also bounds the elementary recursive functions.
The word "Pentation" was coined by Reuben Goodstein
from the roots penta- (five) and iteration
). It is part of his general naming scheme for hyperoperation
s.
Pentation can be written in Knuth's up-arrow notation
as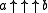 or
or 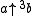 .
.
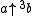 can be done when b is negative or 0 for some small integers. For all positive integer values of a negative pentation is as follows:
can be done when b is negative or 0 for some small integers. For all positive integer values of a negative pentation is as follows:
Any other case of this type of pentation produces an undefined
result, since integer tetration does not take on the value -1.
It can also be done when a is negative, but this is only the case when a is equal to -1. For all positive integer values of b, the three possible answers that you can get for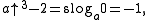 are shown below:
are shown below:
If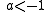 ,
, 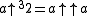 is undefined because tetration is only defined for b greater than -2, while if a is zero, we obtain the presumably-indeterminate form
is undefined because tetration is only defined for b greater than -2, while if a is zero, we obtain the presumably-indeterminate form
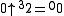 .
.
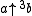 is currently only defined for integer values of a and b where a > 0 and b ≥ 0, and a few other integer values which may be uniquely defined. Like all other hyperoperation
is currently only defined for integer values of a and b where a > 0 and b ≥ 0, and a few other integer values which may be uniquely defined. Like all other hyperoperation
s of order 3 (exponentiation
) and higher, pentation has the following trivial cases (identities) which holds for all values of a and b within its domain:
Other than the trivial cases shown above, pentation generates extremely large numbers very quickly such that there are only a few non-trivial cases that produce numbers that can be written in conventional notation, as illustrated below:
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
, just as tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
is the operation of repeated exponentation and is a hyperoperation
Hyperoperation
In mathematics, the hyperoperation sequenceis an infinite sequence of arithmetic operations that starts with the unary operation of successor, then continues with the binary operations of addition, multiplication and exponentiation, after which the sequence proceeds with further binary operations...
. It is non-commutative, and therefore has two inverse functions, which might be named the penta-root and the penta-logarithm (analogous to the two inverse functions for exponentiation: nth root
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
function and logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
). Pentation also bounds the elementary recursive functions.
The word "Pentation" was coined by Reuben Goodstein
Reuben Goodstein
Reuben Louis Goodstein was an English mathematician with a strong interest in the philosophy and teaching of mathematics....
from the roots penta- (five) and iteration
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
). It is part of his general naming scheme for hyperoperation
Hyperoperation
In mathematics, the hyperoperation sequenceis an infinite sequence of arithmetic operations that starts with the unary operation of successor, then continues with the binary operations of addition, multiplication and exponentiation, after which the sequence proceeds with further binary operations...
s.
Pentation can be written in Knuth's up-arrow notation
Knuth's up-arrow notation
In mathematics, Knuth's up-arrow notation is a method of notation for very large integers, introduced by Donald Knuth in 1976. It is closely related to the Ackermann function and especially to the hyperoperation sequence. The idea is based on the fact that multiplication can be viewed as iterated...
as
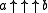 or
or 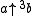 .
.Extension
It is not known how to extend pentation to complex or non-integer values.Extension to zero and negative numbers
Using super-logarithms,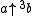 can be done when b is negative or 0 for some small integers. For all positive integer values of a negative pentation is as follows:
can be done when b is negative or 0 for some small integers. For all positive integer values of a negative pentation is as follows:Any other case of this type of pentation produces an undefined
Undefined
Undefined may refer to:* Something that lacks definition* In mathematics, something which lacks well-definition* In calculus, an indeterminate form* Undefined citizenship, a term used sometimes for statelessness- In computing :...
result, since integer tetration does not take on the value -1.
It can also be done when a is negative, but this is only the case when a is equal to -1. For all positive integer values of b, the three possible answers that you can get for
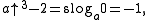 are shown below:
are shown below:-
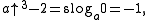 if b is congruent to 1 modulo 3.
if b is congruent to 1 modulo 3. -
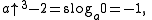 if b is congruent to 2 modulo 3.
if b is congruent to 2 modulo 3. -
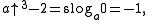 if b is congruent to 0 modulo 3.
if b is congruent to 0 modulo 3.
If
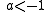 ,
, 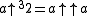 is undefined because tetration is only defined for b greater than -2, while if a is zero, we obtain the presumably-indeterminate form
is undefined because tetration is only defined for b greater than -2, while if a is zero, we obtain the presumably-indeterminate formIndeterminate form
In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...
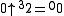 .
.Selected values
As its base operation (tetration) has not been extended to non-integer heights, pentation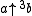 is currently only defined for integer values of a and b where a > 0 and b ≥ 0, and a few other integer values which may be uniquely defined. Like all other hyperoperation
is currently only defined for integer values of a and b where a > 0 and b ≥ 0, and a few other integer values which may be uniquely defined. Like all other hyperoperationHyperoperation
In mathematics, the hyperoperation sequenceis an infinite sequence of arithmetic operations that starts with the unary operation of successor, then continues with the binary operations of addition, multiplication and exponentiation, after which the sequence proceeds with further binary operations...
s of order 3 (exponentiation
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
) and higher, pentation has the following trivial cases (identities) which holds for all values of a and b within its domain:
Other than the trivial cases shown above, pentation generates extremely large numbers very quickly such that there are only a few non-trivial cases that produce numbers that can be written in conventional notation, as illustrated below:
-
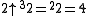
-

-
 (shown here in iterated exponential notation as it's far too large to be written in conventional notation. Note
(shown here in iterated exponential notation as it's far too large to be written in conventional notation. Note 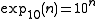 )
) -
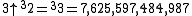
-
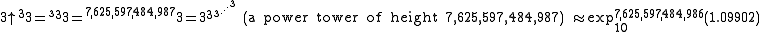
-
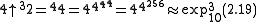 (a number with over 10153 digits)
(a number with over 10153 digits) -
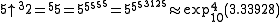 (a number with more than 10102184 digits)
(a number with more than 10102184 digits)