
Perron's formula
Encyclopedia
In mathematics
, and more particularly in analytic number theory
, Perron's formula is a formula due to Oskar Perron
to calculate the sum of an arithmetical function, by means of an inverse Mellin transform
.
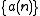 be an arithmetic function
be an arithmetic function
, and let
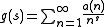
be the corresponding Dirichlet series. Presume the Dirichlet series to be absolutely convergent for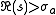 . Then Perron's formula is
. Then Perron's formula is
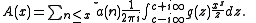
Here, the star on the summation indicates that the last term of the sum must be multiplied by 1/2 when x is an integer. The formula requires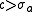 and
and 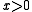 real, but otherwise arbitrary.
real, but otherwise arbitrary.
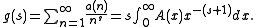
This is nothing but a Laplace transform under the variable change Inverting it one gets the Perron's formula.
Inverting it one gets the Perron's formula.
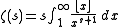
and a similar formula for Dirichlet L-functions:
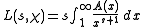
where
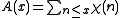
and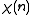 is a Dirichlet character
is a Dirichlet character
. Other examples appear in the articles on the Mertens function and the von Mangoldt function
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and more particularly in analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
, Perron's formula is a formula due to Oskar Perron
Oskar Perron
Oskar Perron was a German mathematician.He was a professor at the University of Heidelberg from 1914 to 1922 and at the University of Munich from 1922 to 1951...
to calculate the sum of an arithmetical function, by means of an inverse Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
.
Statement
Let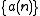 be an arithmetic function
be an arithmetic functionArithmetic function
In number theory, an arithmetic function is a real or complex valued function ƒ defined on the set of natural numbers In number theory, an arithmetic (or arithmetical) function is a real or complex valued function ƒ(n) defined on the set of natural numbers In number theory, an arithmetic (or...
, and let
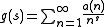
be the corresponding Dirichlet series. Presume the Dirichlet series to be absolutely convergent for
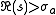 . Then Perron's formula is
. Then Perron's formula is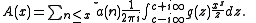
Here, the star on the summation indicates that the last term of the sum must be multiplied by 1/2 when x is an integer. The formula requires
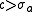 and
and 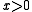 real, but otherwise arbitrary.
real, but otherwise arbitrary.Proof
An easy sketch of the proof comes from taking the Abel's sum formula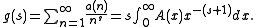
This is nothing but a Laplace transform under the variable change
 Inverting it one gets the Perron's formula.
Inverting it one gets the Perron's formula.Examples
Because of its general relationship to Dirichlet series, the formula is commonly applied to many number-theoretic sums. Thus, for example, one has the famous integral representation for the Riemann zeta function: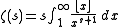
and a similar formula for Dirichlet L-functions:
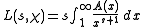
where
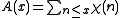
and
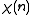 is a Dirichlet character
is a Dirichlet characterDirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
. Other examples appear in the articles on the Mertens function and the von Mangoldt function
Von Mangoldt function
In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt.-Definition:The von Mangoldt function, conventionally written as Λ, is defined as...
.

