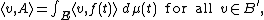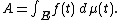Pettis integral
Encyclopedia
In mathematics
, the Pettis integral or Gelfand–Pettis integral, named after I. M. Gelfand
and B.J. Pettis
, extends the definition of the Lebesgue integral to functions on a measure space which take values in a Banach space
, by the use of duality
. The integral was introduced by Gelfand for the case when the measure space is an interval with Lebesgue measure
. The integral is also called the weak integral in contrast to the Bochner integral
, which is the strong integral.
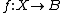, where 
is a measure space, 
, and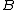 
is a Banach space. If 
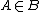exists such that
where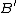
is the dual space
of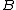
, then 
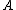is the Pettis integral of 
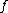over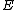 
, and we write
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Pettis integral or Gelfand–Pettis integral, named after I. M. Gelfand
Israel Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
and B.J. Pettis
Billy James Pettis
Billy James Pettis , was an American mathematician, known for his contributions to functional analysis.-See also:*Dunford–Pettis property*Dunford–Pettis theorem*Milman–Pettis theorem*Orlicz–Pettis theorem*Pettis integral...
, extends the definition of the Lebesgue integral to functions on a measure space which take values in a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, by the use of duality
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
. The integral was introduced by Gelfand for the case when the measure space is an interval with Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. The integral is also called the weak integral in contrast to the Bochner integral
Bochner integral
In mathematics, the Bochner integral, named for Salomon Bochner, extends the definition of Lebesgue integral to functions that take values in a Banach space, as the limit of integrals of simple functions.-Definition:...
, which is the strong integral.
Definition
Suppose that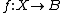, where is a measure space, , and 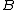is a Banach space. If 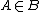exists such that
where
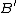is the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of
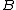, then 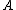is the Pettis integral of 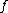over 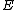, and we write
