Phase noise
Encyclopedia
Phase noise is the frequency domain
representation of rapid, short-term, random fluctuations in the phase
of a waveform
, caused by time domain
instabilities ("jitter
"). Generally speaking, radio frequency engineers speak of the phase noise of an oscillator, whereas digital system engineers work with the jitter of a clock.
Historically there have been two conflicting yet widely used definitions for phase noise. The definition used by some authors defines phase noise to be the Power Spectral Density
(PSD) of a signal's phase, the other one is based on the PSD of the signal itself. Both definitions yield the same result at offset frequencies well removed from the carrier. At close-in offsets however, characterization results strongly depends on the chosen definition. Recently, the IEEE changed its official definition to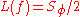
where 
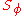is the (single-sided) spectral density of a signal's phase fluctuations.
An ideal oscillator
would generate a pure sine wave
. In the frequency domain, this would be represented as a single pair of delta functions (positive and negative conjugates) at the oscillator's frequency, i.e., all the signal's power
is at a single frequency. All real oscillators have phase modulated noise
components. The phase noise components spread the power of a signal to adjacent frequencies, resulting in noise sidebands. Oscillator phase noise often includes low frequency flicker noise
and may include white noise
.
Consider the following noise free signal:
Phase noise is added to this signal by adding a stochastic process
represented by φ to the signal as follows:
Phase noise is a type of cyclostationary noise and is closely related to jitter
. A particularly important type of phase noise is that produced by oscillators
.
Phase noise (L(f)) is typically expressed in units of dBc
/Hz, representing the noise power relative to the carrier contained in a 1 Hz bandwidth centered at a certain offsets from the carrier. For example, a certain signal may have a phase noise of -80 dBc/Hz at an offset of 10 kHz and -95 dBc/Hz at an offset of 100 kHz. Phase noise can be measured and expressed as single sideband or double sideband values, but as noted earlier, the IEEE has adapted as its official definition, one-half the double sideband PSD.
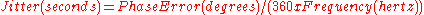
In the absence of 1/f noise in a region where the phase noise displays a –20 dBc/Hz slope, the
rms cycle jitter can be related to the phase noise by:
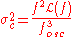
Likewise:
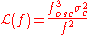
if the phase noise of the device under test (DUT) is large with respect to the spectrum analyzer's local oscillator
. Care should be taken that observed values are due to the measured signal and not the Shape Factor of the spectrum analyzer's filters. Spectrum analyzer based measurement can show the phase-noise power over many decades of frequency e.g. 1 Hz to 10 MHz. The slope with offset frequency in various offset frequency regions can provide clues as to the source of the noise, e.g. low frequency flicker noise
decreasing at 30 dB per decade (=9 dB per octave).
is a single line in the frequency spectrum. Such perfect spectral purity is not achievable in a practical oscillator. Spreading of the spectrum line caused by phase noise must be minimised in the local oscillator for a superheterodyne receiver
because it defeats the aim of restricting the receiver frequency range by filters in the IF (intermediate frequency) amplifier.
Frequency domain
In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
representation of rapid, short-term, random fluctuations in the phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
of a waveform
Waveform
Waveform means the shape and form of a signal such as a wave moving in a physical medium or an abstract representation.In many cases the medium in which the wave is being propagated does not permit a direct visual image of the form. In these cases, the term 'waveform' refers to the shape of a graph...
, caused by time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
instabilities ("jitter
Jitter
Jitter is the undesired deviation from true periodicity of an assumed periodic signal in electronics and telecommunications, often in relation to a reference clock source. Jitter may be observed in characteristics such as the frequency of successive pulses, the signal amplitude, or phase of...
"). Generally speaking, radio frequency engineers speak of the phase noise of an oscillator, whereas digital system engineers work with the jitter of a clock.
Historically there have been two conflicting yet widely used definitions for phase noise. The definition used by some authors defines phase noise to be the Power Spectral Density
Spectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
(PSD) of a signal's phase, the other one is based on the PSD of the signal itself. Both definitions yield the same result at offset frequencies well removed from the carrier. At close-in offsets however, characterization results strongly depends on the chosen definition. Recently, the IEEE changed its official definition to
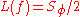where 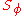is the (single-sided) spectral density of a signal's phase fluctuations.An ideal oscillator
Electronic oscillator
An electronic oscillator is an electronic circuit that produces a repetitive electronic signal, often a sine wave or a square wave. They are widely used in innumerable electronic devices...
would generate a pure sine wave
Sine wave
The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
. In the frequency domain, this would be represented as a single pair of delta functions (positive and negative conjugates) at the oscillator's frequency, i.e., all the signal's power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
is at a single frequency. All real oscillators have phase modulated noise
Electronic noise
Electronic noise is a random fluctuation in an electrical signal, a characteristic of all electronic circuits. Noise generated by electronic devices varies greatly, as it can be produced by several different effects...
components. The phase noise components spread the power of a signal to adjacent frequencies, resulting in noise sidebands. Oscillator phase noise often includes low frequency flicker noise
Flicker noise
Flicker noise is a type of electronic noise with a 1/ƒ, or pink power density spectrum. It is therefore often referred to as 1/ƒ noise or pink noise, though these terms have wider definitions...
and may include white noise
White noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
.
Consider the following noise free signal:
- v(t) = Acos(2πf0t).
Phase noise is added to this signal by adding a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
represented by φ to the signal as follows:
- v(t) = Acos(2πf0t + φ(t)).
Phase noise is a type of cyclostationary noise and is closely related to jitter
Jitter
Jitter is the undesired deviation from true periodicity of an assumed periodic signal in electronics and telecommunications, often in relation to a reference clock source. Jitter may be observed in characteristics such as the frequency of successive pulses, the signal amplitude, or phase of...
. A particularly important type of phase noise is that produced by oscillators
Oscillator Phase Noise
Oscillators inherently produce high levels of phase noise. That noise increases at frequencies close to the oscillation frequency or its harmonics. With the noise being close to the oscillation frequency, it cannot be removed by filtering without also removing the oscillation signal...
.
Phase noise (L(f)) is typically expressed in units of dBc
DBc
dBc is the power ratio of a signal to a carrier signal, expressed in decibels. For example, phase noise is expressed in dBc/Hz at a given frequency offset from the carrier...
/Hz, representing the noise power relative to the carrier contained in a 1 Hz bandwidth centered at a certain offsets from the carrier. For example, a certain signal may have a phase noise of -80 dBc/Hz at an offset of 10 kHz and -95 dBc/Hz at an offset of 100 kHz. Phase noise can be measured and expressed as single sideband or double sideband values, but as noted earlier, the IEEE has adapted as its official definition, one-half the double sideband PSD.
Jitter Conversions
Phase noise is sometimes also measured and expressed as a power obtained by integrating L(f) over a certain range of offset frequencies. For example, the phase noise may be -40 dBc integrated over the range of 1 kHz to 100 kHz. This Integrated phase noise (expressed in degrees) can be converted to jitter (expressed in seconds) using the following formula.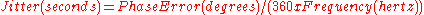In the absence of 1/f noise in a region where the phase noise displays a –20 dBc/Hz slope, the
rms cycle jitter can be related to the phase noise by:
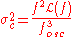
Likewise:
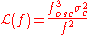
Measurement
Phase noise can be measured using a spectrum analyzerSpectrum analyzer
A spectrum analyzer measures the magnitude of an input signal versus frequency within the full frequency range of the instrument. The primary use is to measure the power of the spectrum of known and unknown signals...
if the phase noise of the device under test (DUT) is large with respect to the spectrum analyzer's local oscillator
Local oscillator
A local oscillator is an electronic device used to generate a signal normally for the purpose of converting a signal of interest to a different frequency using a mixer. This process of frequency conversion, also referred to as heterodyning, produces the sum and difference frequencies of the...
. Care should be taken that observed values are due to the measured signal and not the Shape Factor of the spectrum analyzer's filters. Spectrum analyzer based measurement can show the phase-noise power over many decades of frequency e.g. 1 Hz to 10 MHz. The slope with offset frequency in various offset frequency regions can provide clues as to the source of the noise, e.g. low frequency flicker noise
Flicker noise
Flicker noise is a type of electronic noise with a 1/ƒ, or pink power density spectrum. It is therefore often referred to as 1/ƒ noise or pink noise, though these terms have wider definitions...
decreasing at 30 dB per decade (=9 dB per octave).
Spectral purity
The sinewave output of an ideal oscillatorElectronic oscillator
An electronic oscillator is an electronic circuit that produces a repetitive electronic signal, often a sine wave or a square wave. They are widely used in innumerable electronic devices...
is a single line in the frequency spectrum. Such perfect spectral purity is not achievable in a practical oscillator. Spreading of the spectrum line caused by phase noise must be minimised in the local oscillator for a superheterodyne receiver
Superheterodyne receiver
In electronics, a superheterodyne receiver uses frequency mixing or heterodyning to convert a received signal to a fixed intermediate frequency, which can be more conveniently processed than the original radio carrier frequency...
because it defeats the aim of restricting the receiver frequency range by filters in the IF (intermediate frequency) amplifier.
External links
- The site http://rubiola.org contains a bunch of information and literature about phase noise, frequency stability, experimental techniques, etc.
- A technical article about phase noise in signal sources due to phase modulation.
- Phase-noise measurement software for various GPIB-equipped spectrum analyzers (freeware, includes Win32 C++ source)
- Clock (CLK) Jitter and Phase Noise Conversion
- Phase noise and frequency synthesizers
- Phase Noise measurement using the phase lock technique
- Noise in Mixers, Oscillators, Samplers, and Logic: An Introduction to Cyclostationary Noise by Joel Phillips and Ken Kundert
- Predicting the phase noise and jitter of PLL-based frequency synthesizers by Ken Kundert
- Y. T. Su, K. T. Wong & K.-P. Ho, "Linear MMSE Estimation of Large-Magnitude Symmetric Levy-Process Phase-Noise", IEEE Transactions on Communications.
Further reading
- Rubiola, Enrico 2008. Phase Noise and Frequency Stability in Oscillators, Cambridge University Press, ISBN 978-0-521-88677-2
- Wolaver, Dan H. 1991. Phase-Locked Loop Circuit Design, Prentice Hall, ISBN 0-13-662743-9
- M. Lax, "Classical noise. V. Noise in self-sustained oscillators", Physical Review, vol. 160, p. 290, August 1967, DOI 10.1103/PhysRev.160.290
- A. Hajimiri and T.H. Lee, "A general theory of phase noise in electrical oscillators", IEEE Journal of Solid-State Circuits, Vol. 33, No 2, Feb. 1998 Pages:179 - 194, DOI 10.1109/4.658619
- R. Pulikkoonattu, "Oscilattor Phase Noise and Sampling Clock Jitter http://documents.epfl.ch/users/p/pu/pulikkoo/private/report_pn_jitter_oscillator_ratna.pdf", ST Microelectronics Tech Note., DOI 08.09.2007
- A. Demir, A. Mehrotra and J. Roychowdhury, "Phase noise in oscillators: a unifying theory and numerical methods for characterization", IEEE Trans. on Circuits and Systems I: Fundamental Theory and Applications, Vol. 47, No 5, May 2000, Pages:655 - 674, DOI 10.1109/81.847872
- A. Chorti and M. Brookes, "A spectral model for RF oscillators with power-law phase noise", IEEE Trans. on Circuits and Systems I: Regular Papers, Vol. 53, No 9, Sept. 2006 Pages:1989 - 1999, DOI 10.1109/TCSI.2006.881182