
Pick's theorem
Encyclopedia
Given a simple polygon
constructed on a grid of equal-distanced points (i.e., points with integer
coordinates) such that all the polygon's vertices are grid points, Pick's theorem provides a simple formula
for calculating the area
A of this polygon in terms of the number i of lattice points in the interior located in the polygon and the number b of lattice points on the boundary placed on the polygon's perimeter:

In the example shown, we have i = 7 interior points and b = 8 boundary points, so the area is A = 7 + 8/2 − 1 = 7 + 4 − 1 = 10 (square units)
Note that the theorem as stated above is only valid for simple polygons, i.e., ones that consist of a single piece and do not contain "holes". For a polygon that has h holes, with a boundary in the form of h + 1 simple closed curves, the slightly more complicated formula i + b/2 + h − 1 gives the area.
The result was first described by Georg Alexander Pick
in 1899. The Reeve tetrahedron
shows that there is no analogue of Pick's theorem in three dimensions that expresses the volume of a polytope by counting its interior and boundary points. However, there is a generalization in higher dimensions via Ehrhart polynomial
s. The formula also generalizes to surfaces of polyhedra
.
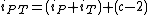
and

From the above follows

and

Since we are assuming the theorem for P and for T separately,
Simple polygon
In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
constructed on a grid of equal-distanced points (i.e., points with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coordinates) such that all the polygon's vertices are grid points, Pick's theorem provides a simple formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
for calculating the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
A of this polygon in terms of the number i of lattice points in the interior located in the polygon and the number b of lattice points on the boundary placed on the polygon's perimeter:

In the example shown, we have i = 7 interior points and b = 8 boundary points, so the area is A = 7 + 8/2 − 1 = 7 + 4 − 1 = 10 (square units)
Note that the theorem as stated above is only valid for simple polygons, i.e., ones that consist of a single piece and do not contain "holes". For a polygon that has h holes, with a boundary in the form of h + 1 simple closed curves, the slightly more complicated formula i + b/2 + h − 1 gives the area.
The result was first described by Georg Alexander Pick
Georg Alexander Pick
Georg Alexander Pick was an Austrian mathematician. He was born to Josefa Schleisinger and Adolf Josef Pick. He died in the Theresienstadt concentration camp. Today he is best known for Pick's formula for determining the area of lattice polygons...
in 1899. The Reeve tetrahedron
Reeve tetrahedron
In geometry, the Reeve tetrahedron is a polyhedron, named after John Reeve, in R3 with vertices at , , and where r is a positive integer. Each vertex lies on a fundamental lattice point...
shows that there is no analogue of Pick's theorem in three dimensions that expresses the volume of a polytope by counting its interior and boundary points. However, there is a generalization in higher dimensions via Ehrhart polynomial
Ehrhart polynomial
In mathematics, an integral polytope has an associated Ehrhart polynomial which encodes the relationship between the volume of a polytope and the number of integer points the polytope contains...
s. The formula also generalizes to surfaces of polyhedra
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
.
Proof
Consider a polygon P and a triangle T, with one edge in common with P. Assume Pick's theorem is true for P; we want to show that it is also true to the polygon PT obtained by adding T to P. Since P and T share an edge, all the boundary points along the edge in common are merged to interior points, except for the two endpoints of the edge, which are merged to boundary points. So, calling the number of boundary points in common c, we have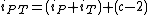
and

From the above follows

and

Since we are assuming the theorem for P and for T separately,
-

Therefore, if the theorem is true for polygons constructed from n triangles, the theorem is also true for polygons constructed from n + 1 triangles. For general polytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s, it is well known that they can always be triangulated. That this is true in dimension 2 is an easy fact.
To finish the proof by mathematical inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, it remains to show that the theorem is true for triangles. The verification for this case can be done in these short steps:
- observe that the formula holds for any unit square (with vertices having integer coordinates);
- deduce from this that the formula is correct for any rectangleRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
with sides parallelParallel (geometry)Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
to the axes; - deduce it, now, for right-angled triangles obtained by cutting such rectangles along a diagonalDiagonalA diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
; - now any triangle can be turned into a rectangle by attaching (at most three) such right triangles; since the formula is correct for the right triangles and for the rectangle, it also follows for the original triangle.
The last step uses the fact that if the theorem is true for the polygon PT and for the triangle T, then it's also true for P; this can be seen by a calculation very much similar to the one shown above.
External links
- Pick's Theorem (Java) at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Pick's Theorem
- Pick's Theorem proof by Tom Davis
- Pick's Theorem by Ed Pegg, Jr.Ed Pegg, Jr.Ed Pegg, Jr. is an expert on mathematical puzzles and is a self-described recreational mathematician. He creates puzzles for the Mathematical Association of America online at Ed Pegg, Jr.'s Math Games. His puzzles have also been used by Will Shortz on the puzzle segment of NPR's Weekend Edition...
, the Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
.

