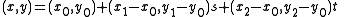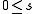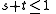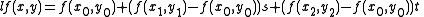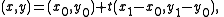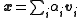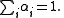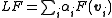Piecewise linear continuation
Encyclopedia
Simplicial Continuation
Simplicial Continuation, or Piecewise Linear Continuation (Allgower and Georg [1], [3]) is a one parameter continuation methodNumerical continuation
Numerical continuation is a method of computing approximate solutions of a system of parameterized nonlinear equations,F = 0The parameter \lambda is usually a real scalar, and the solution an n-vector...
which is well suited to small to medium embedding spaces. The algorithm has been generalized to compute higher dimensional manifolds by (Allgower and Gnutzman [2]) and (Allgower and Schmidt [4]).
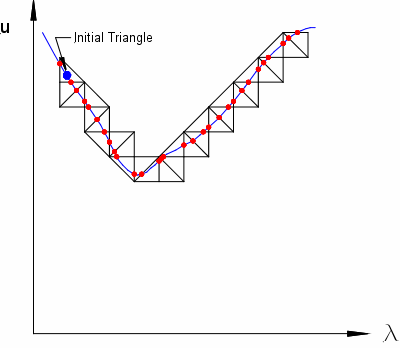
The algorithm for drawing contours is a simplicial continuation algorithm, and since it is easy to visualize, it serves as a good introduction to the algorithm.
Contour Plotting
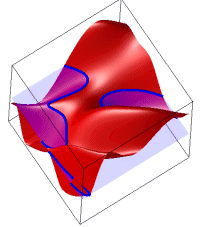
The contour plotting problem is to find the zeros (contours) of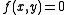 (
(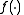 a smooth scalar valued function) in the square
a smooth scalar valued function) in the square 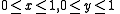 ,
,
The square is divided into small triangles, usually by introducing points at the corners of a regular square mesh
 ,
, 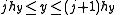 , making a table of the values of
, making a table of the values of 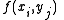 at each corner
at each corner 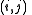 , and then dividing each square into two triangles. The value of
, and then dividing each square into two triangles. The value of 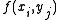 at the corners of the triangle defines a unique Piecewise Linear interpolant
at the corners of the triangle defines a unique Piecewise Linear interpolant 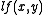 to
to 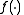 over each triangle. One way of writing this interpolant on the triangle with corners
over each triangle. One way of writing this interpolant on the triangle with corners is as the set of equations
is as the set of equationsThe first four equations can be solved for
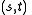 (this maps the original triangle to a right unit triangle), then the remaining equation gives the interpolated value of
(this maps the original triangle to a right unit triangle), then the remaining equation gives the interpolated value of 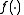 . Over the whole mesh of triangles, this piecewise linear interpolant is continuous.
. Over the whole mesh of triangles, this piecewise linear interpolant is continuous.
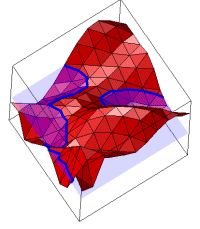
The contour of the interpolant on an individual triangle is a line segment (it is an interval on the intersection of two planes). The equation for the line can be found, however the points where the line crosses the edges of the triangle are the endpoints of the line segment.
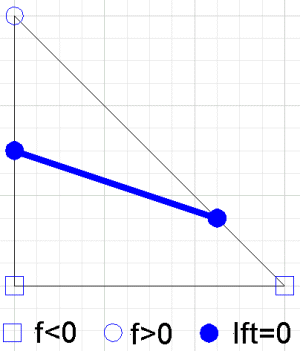
The contour of the piecewise linear interpolant is a set of curves made up of these line segments. Any point on the edge connecting
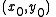 and
and 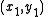 can be written as
can be written aswith
 in
in 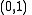 , and the linear interpolant over the edge is
, and the linear interpolant over the edge isSo setting
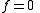
-
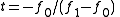 and
and 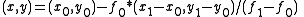
Since this only depends on values on the edge, every triangle which shares this edge will produce the same point, so the contour will be continuous. Each triangle can be tested independently, and if all are checked the entire set of contour curves can be found.
Piecewise Linear Continuation
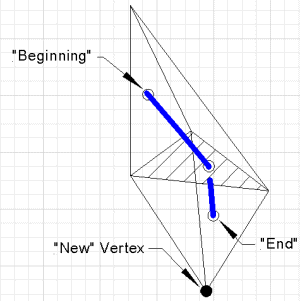
Piecewise linear continuation is similar to contour plotting (Dobkin, Silvio, Thurston and Wilks [5]), but in higher dimensions. The algorithm is based on the following results:Lemma 1
If F(x) maps 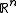 into into 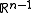 , there is a unique linear interpolant on an '(n-1)'-dimensional simplex , there is a unique linear interpolant on an '(n-1)'-dimensional simplexSimplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... which agrees with the function values at the vertices of the simplex. |
An '(n-1)'-dimensional simplex has n vertices, and the function F assigns an 'n'-vector to each. The simplex is convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, and any point within the simplex is a convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of the vertices. That is
If x is in the interior of an (n-1)-dimensional simplex with n vertices
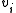 , then there are positive scalars
, then there are positive scalars  such that
such thatIf the vertices of the simplex are linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
the non-negative scalars
 are unique for each point x, and are called the barycentric coordinates
are unique for each point x, and are called the barycentric coordinatesBarycentric coordinates (mathematics)
In geometry, the barycentric coordinate system is a coordinate system in which the location of a point is specified as the center of mass, or barycenter, of masses placed at the vertices of a simplex . Barycentric coordinates are a form of homogeneous coordinates...
of x. They determine the value of the unique interpolant
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
by the formula:
Lemma 2
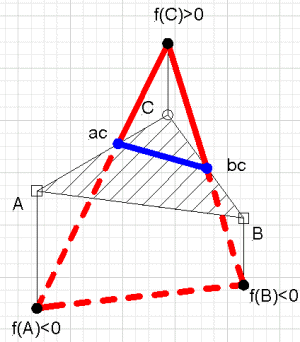
| An (n-1)-dimensional simplex can be tested to determine if it contains the origin. |
There are basically two tests. The one which was first used labels the vertices of the simplex with a vector of signs (+/-) of the coordinates of the vertex. For example the vertex (.5,-.2,1.) would be labelled (+,-,+). A simplex is called completely labelled if there is a vertex whose label begins with a string of "+" signs of length 0,1,2,3,4,...n. A completely labelled simplex contains a neighborhood of the origin. This may be surprising, but what underlies this result is that for each coordinate of a completely labelled simplex there is a vector with "+" and another with a "-". Put another way, the smallest cube with edges parallel to the coordinate axes and which covers the simplex has pairs of faces on opposite sides of 0. (i.e. a "+" and a "-" for each coordinate.).
The second approach is called vector labelling. It is based on the barycentric coordindates of the vertices of the simplex. The first step is to find the barycentric coordinates of the origin, and then the test that the simplex contains the origin is simply that all the barycentric coordinates are positive and the sum is less than 1.
Lemma 3
There is a triangulation (the Coxeter-Freudenthal-Kuhn triangulation [1]) which is invariant under the pivot operation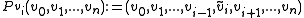 where  |