
Pierce–Birkhoff conjecture
Encyclopedia
In abstract algebra
, the Pierce–Birkhoff conjecture asserts that any piecewise-polynomial function can be expressed as a maximum
of finite minima
of finite collections of polynomial
s. It was first stated, albeit in non-rigorous and vague wording, in the 1956 paper of Garrett Birkhoff
and Richard S. Pierce in which they first introduced f-rings. The modern, rigorous statement of the conjecture was formulated by Melvin Henriksen and John R. Isbell
, who worked on the problem in the early 1960s in connection with their work on f-rings. Their formulation is as follows:
Isbell is likely the source of the name Pierce–Birkhoff conjecture, and popularized the problem in the 1980s by discussing it with several mathematicians interested in real algebraic geometry
.
The conjecture was proved true for n = 1 and 2 by Louis Mahé.
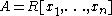 and the novel concepts of local polynomial representatives and separating ideals.
and the novel concepts of local polynomial representatives and separating ideals.
Denoting the real spectrum of A by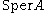 , the separating ideal of α and β in
, the separating ideal of α and β in 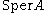 is the ideal of A generated by all polynomials
is the ideal of A generated by all polynomials 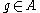 that change sign on α and β, ie.
that change sign on α and β, ie. 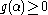 and
and 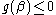 . Any finite covering
. Any finite covering 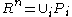 of closed
of closed
, semi-algebraic sets induces a corresponding covering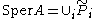 , so, in particular, when f is piecewise polynomial, there is a polynomial
, so, in particular, when f is piecewise polynomial, there is a polynomial 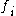 for every
for every 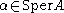 such that
such that 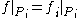 and
and 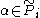 . This
. This 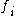 is termed the local polynomial representative of f at α.
is termed the local polynomial representative of f at α.
Madden's so-called local Pierce–Birkhoff conjecture at α and β, which is equivalent to the Pierce–Birkhoff conjecture, is as follows:
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the Pierce–Birkhoff conjecture asserts that any piecewise-polynomial function can be expressed as a maximum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of finite minima
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of finite collections of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s. It was first stated, albeit in non-rigorous and vague wording, in the 1956 paper of Garrett Birkhoff
Garrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
and Richard S. Pierce in which they first introduced f-rings. The modern, rigorous statement of the conjecture was formulated by Melvin Henriksen and John R. Isbell
John R. Isbell
John Rolfe Isbell was an American mathematician, for many years a professor of mathematics at the University of Buffalo .-Biography:...
, who worked on the problem in the early 1960s in connection with their work on f-rings. Their formulation is as follows:
- for every real piecewise-polynomial function
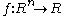 , there exists a finite set of polynomials
, there exists a finite set of polynomials 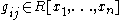 such that
such that 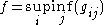 .
.
Isbell is likely the source of the name Pierce–Birkhoff conjecture, and popularized the problem in the 1980s by discussing it with several mathematicians interested in real algebraic geometry
Real algebraic geometry
In mathematics, real algebraic geometry is the study of real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them ....
.
The conjecture was proved true for n = 1 and 2 by Louis Mahé.
Local Pierce–Birkhoff conjecture
In 1989, James J. Madden provided an equivalent statement that is in terms of the real spectrum of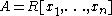 and the novel concepts of local polynomial representatives and separating ideals.
and the novel concepts of local polynomial representatives and separating ideals.Denoting the real spectrum of A by
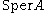 , the separating ideal of α and β in
, the separating ideal of α and β in 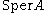 is the ideal of A generated by all polynomials
is the ideal of A generated by all polynomials 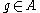 that change sign on α and β, ie.
that change sign on α and β, ie. 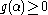 and
and 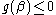 . Any finite covering
. Any finite covering 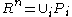 of closed
of closedClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
, semi-algebraic sets induces a corresponding covering
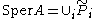 , so, in particular, when f is piecewise polynomial, there is a polynomial
, so, in particular, when f is piecewise polynomial, there is a polynomial 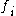 for every
for every 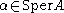 such that
such that 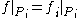 and
and 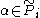 . This
. This 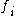 is termed the local polynomial representative of f at α.
is termed the local polynomial representative of f at α.Madden's so-called local Pierce–Birkhoff conjecture at α and β, which is equivalent to the Pierce–Birkhoff conjecture, is as follows:
- Let α, β be in
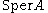 and f be piecewise-polynomial. It is conjectured that for every local representative of f at α,
and f be piecewise-polynomial. It is conjectured that for every local representative of f at α,  , and local representative of f at β,
, and local representative of f at β, 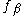 ,
,  is in the separating ideal of α and β.
is in the separating ideal of α and β.

