Planimeter
Encyclopedia
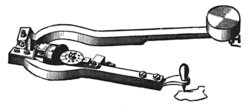
Measuring instrument
In the physical sciences, quality assurance, and engineering, measurement is the activity of obtaining and comparing physical quantities of real-world objects and events. Established standard objects and events are used as units, and the process of measurement gives a number relating the item...
used to determine the area of an arbitrary two-dimensional shape.
Construction
There are several kinds of planimeters, but all operate in a similar way. The precise way in which they are constructed varies, with the main types of mechanical planimeter being polar, linear and Prytz or "hatchet" planimeters. The Swiss mathematicianMathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Jakob Amsler-Laffon
Jakob Amsler-Laffon
Jakob Amsler-Laffon was a mathematician, physicist, engineer and the founder of his own factory . Amsler was born on the Stalden near the village of Schinznach in the district of Brugg, canton Aargau, and died in Schaffhausen, Switzerland...
built the first modern planimeter in 1854, the concept having been pioneered by Johann Martin Hermann in 1814. Many developments followed Amsler's famous planimeter, including electronic versions.
They consist of a linkage
Linkage (mechanical)
A mechanical linkage is an assembly of bodies connected together to manage forces and movement. The movement of a body, or link, is studied using geometry so the link is considered to be rigid. The connections between links are modeled as providing ideal movement, pure rotation or sliding for...
with a pointer on one end, used to trace around the boundary of the shape. The other end of the linkage is fixed for a polar planimeter and restricted to a line for a linear planimeter. Tracing around the perimeter of a surface induces a movement in another part of the instrument and a reading of this is used to establish the area of the shape. The planimeter contains a measuring wheel that rolls along the drawing as the operator traces the contour. When the planimeter's measuring wheel moves perpendicular to its axis, it rolls, and this movement is recorded. When the measuring wheel moves parallel to its axis, the wheel skids without rolling, so this movement is ignored. That means the planimeter measures the distance that its measuring wheel travels, projected perpendicularly to the measuring wheel's axis of rotation. The area of the shape is proportional to the number of turns through which the measuring wheel rotates when the planimeter is traced along the complete perimeter of the shape.
Developments of the planimeter can establish the position of the first moment of area
First moment of area
The first moment of area, sometimes misnamed as the first moment of inertia, is based in the mathematical construct moments in metric spaces, stating that the moment of area equals the summation of area times distance to an axis [Σ]...
(center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
), and even the second moment of area
Second moment of area
The second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...
.
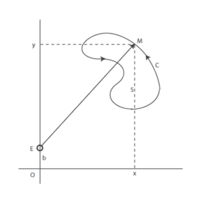
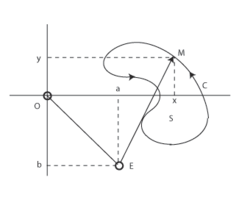
Principle of the linear planimeter
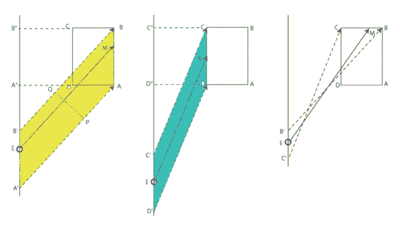
Mathematical derivation
The operation of a linear planimeter can be justified by applying Green's theoremGreen's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
onto the components of the vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
N, given by:
where b is the y-coordinate of the elbow E.
This vector field is perpendicular to the measuring arm EM:
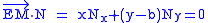
and has a constant size, equal to the length m of the measuring arm:
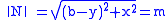
Then:
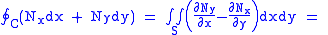
because:
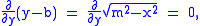
The left hand side of the above equation, which is equal to the area A enclosed by the contour, is proportional to the distance measured by the measuring wheel, with proportionality factor m, the length of the measuring arm.
Polar coordinates
The connection with Green's theorem can be understood in terms of integration in polar coordinates: in polar coordinates, area is computed by the integral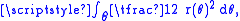
where the form being integrated is quadratic in r, meaning that the rate at which area changes with respect to change in angle varies quadratically with the radius.For a parametric equation
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
in polar coordinates, where both r and θ vary as a function of time, this becomes
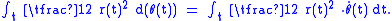
Turning to a planimeter, for a wheel fixed at the end of a link, rotating with respect to a point, the total rotation of the wheel is proportional to
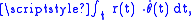as the rotation is proportional to the distance traveled, which at any point in time is proportional to radius and to change in angle, as in the circumference of a circle (
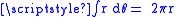).This last integrand
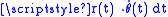can be recognized as the derivative of the earlier integrand 
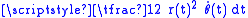(with respect to r) shows that a planimeter computes the area integral in terms of the derivative, which is reflected in Green's theorem, which equates a line integral of a function on a (1-dimensional) contour to the (2-dimensional) integral of the derivative.