Point set triangulation
Encyclopedia
A triangulation of a set of points P in the plane is a triangulation
of the convex hull
of P, with all points from P being among the vertices of the triangulation. Triangulations are special cases of planar straight-line graph
s.
There are special triangulations like the Delaunay triangulation
which is the geometric dual of the Voronoi diagram
. Subsets of the Delaunay triangulation are the Gabriel graph
, nearest neighbor graph
and the minimal spanning tree.
Triangulations have a number of applications, and there is an interest to find a "good" triangulation for a given point set under some criteria. One of them is a minimum-weight triangulation. Sometimes it is desirable to have a triangulation with special properties, e.g., in which all triangles have large angles (long and narrow ("splinter") triangles are avoided).
Given a set of edges that connect some pairs of the points, the problem to determine whether they contain a triangulation is NP-complete
(Lloyd, 1977).
may be derived from of the convex hull
of a set of points S1 in the space of dimension larger by 1 which are the projections of the original point set onto the paraboloid surface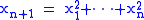
. One has to construct the convex hull of the set S1 and project it back onto the space of S. If points are not in general position, additional effort is required to triangulate the non-tetrahedral facets.
Polygon triangulation
In computational geometry, polygon triangulation is the decomposition of a polygonal area P into a set of triangles, i.e., finding the set of triangles with pairwise non-intersecting interiors whose union is P....
of the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of P, with all points from P being among the vertices of the triangulation. Triangulations are special cases of planar straight-line graph
Planar straight-line graph
Planar straight-line graph is a term used in computational geometry for an embedding of a planar graph in the plane such that its edges are mapped into straight line segments...
s.
There are special triangulations like the Delaunay triangulation
Delaunay triangulation
In mathematics and computational geometry, a Delaunay triangulation for a set P of points in a plane is a triangulation DT such that no point in P is inside the circumcircle of any triangle in DT. Delaunay triangulations maximize the minimum angle of all the angles of the triangles in the...
which is the geometric dual of the Voronoi diagram
Voronoi diagram
In mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
. Subsets of the Delaunay triangulation are the Gabriel graph
Gabriel graph
In mathematics, the Gabriel graph of a set S of points in the Euclidean plane expresses one notion of proximity or nearness of those points. Formally, it is the graph with vertex set S in which any points P and Q in S are adjacent precisely if they are distinct and the closed disc of which line...
, nearest neighbor graph
Nearest neighbor graph
The nearest neighbor graph for a set of n objects P in a metric space is a directed graph with P being its vertex set and with a directed edge from p to q whenever q is a nearest neighbor of p The nearest neighbor graph (NNG) for a set of n objects P in a metric space (e.g., for a set of points...
and the minimal spanning tree.
Triangulations have a number of applications, and there is an interest to find a "good" triangulation for a given point set under some criteria. One of them is a minimum-weight triangulation. Sometimes it is desirable to have a triangulation with special properties, e.g., in which all triangles have large angles (long and narrow ("splinter") triangles are avoided).
Given a set of edges that connect some pairs of the points, the problem to determine whether they contain a triangulation is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
(Lloyd, 1977).
Triangulation and convex hull
A triangulation of the set of points S in general positionGeneral position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
may be derived from of the convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of a set of points S1 in the space of dimension larger by 1 which are the projections of the original point set onto the paraboloid surface
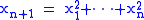. One has to construct the convex hull of the set S1 and project it back onto the space of S. If points are not in general position, additional effort is required to triangulate the non-tetrahedral facets.