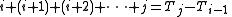Polite number
Encyclopedia
In number theory
, a polite number is a positive integer that can be written as the sum of two or more consecutive positive integers. Other positive integers are impolite.
Polite numbers have also been called staircase numbers because the Young diagrams representing graphically the partition
s of a polite number into consecutive integers (in the French style of drawing these diagrams) resemble staircases. If all numbers in the sum are strictly greater than one, the numbers so formed are also called trapezoidal numbers because they represent patterns of points arranged in a trapezoid
.
The problem of representing numbers as sums of consecutive integers and of counting the number of representations of this type has been studied by Sylvester
, Mason, and Leveque
, as well as by many other more recent authors.
The impolite numbers are exactly the powers of two
. It follows from the Lambek–Moser theorem that the nth polite number is ƒ(n + 1), where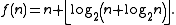
s of x that are greater than one.
The politeness of the numbers 1, 2, 3, ... is
For instance, the politeness of 9 is 2 because it has two odd divisors, 3 and itself, and two polite representations
the politeness of 15 is 3 because it has three odd divisors, 3, 5, and 15, and (as is familiar to cribbage
players) three polite representations
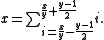
Some of the terms in this sum may be zero or negative. However, if a term is zero it can be omitted and any negative terms may be used to cancel positive ones, leading to a polite representation for x. (The requirement that y > 1 corresponds to the requirement that a polite representation have more than one term; applying the same construction for y = 1 would just lead to the trivial one-term representation x = x.)
For instance, the polite number x = 14 has a single nontrivial odd divisor, 7. It is therefore the sum of 7 consecutive numbers centered at 14/7 = 2:
The first term, −1, cancels a later +1, and the second term, zero, can be omitted, leading to the polite representation
Conversely, every polite representation of x can be formed from this construction. If a representation has an odd number of terms, x/y is the middle term, while if it has an even number of terms and its minimum value is m it may be extended in a unique way to a longer sequence with the same sum and an odd number of terms, by including the 2m − 1 numbers −(m − 1), −(m − 2), ..., −1, 0, 1, ..., −(m − 2), −(m − 1).
After this extension, again, x/y is the middle term. By this construction, the polite representations of a number and its odd divisors greater than one may be placed into a one-to-one correspondence
, giving a bijective proof
of the characterization of polite numbers and politeness. More generally, the same idea gives a two-to-one correspondence between, on the one hand, representations as a sum of consecutive integers (allowing zero, negative numbers, and single-term representations) and on the other hand odd divisors (including 1).
Another generalization of this result states that, for any n, the number of partitions of n into odd numbers having k distinct values equals the number of partitions of n into distinct numbers having k maximal runs of consecutive numbers.
Here a run is one or more consecutive values such that the next larger and the next smaller consecutive values are not part of the partition; for instance the partition 10 = 1 + 4 + 5 has two runs, 1 and 4 + 5.
A polite representation has a single run, and a partition with one value d is equivalent to a factorization of n as the product d×(n/d), so the special case k = 1 of this result states again the equivalence between polite representations and odd factors (including in this case the trivial representation n = n and the trivial odd factor 1).
Otherwise, it is the difference of two triangular numbers:
In the latter case, it is called a trapezoidal number. That is, a trapezoidal number is a polite number that has a polite representation in which all terms are strictly greater than one. The only polite numbers that may be non-trapezoidal are the triangular numbers with only one nontrivial odd divisor, because for those numbers, according to the bijection described earlier, the odd divisor corresponds to the triangular representation and there can be no other polite representations. Thus, polite non-trapezoidal numbers must have the form of a power of two multiplied by a prime number. As Jones and Lord observe, there are exactly two types of triangular numbers with this form:
For instance, the perfect number 28 = 23 − 1(23 − 1) and the number 136 = 24 − 1(24 + 1) are both polite triangular numbers that are not trapezoidal. It is believed that there are finitely many Fermat primes (only five of which — 3, 5, 17, 257, and 65,537 — have been discovered), but infinitely many Mersenne primes, in which case there are also infinitely many polite non-trapezoidal numbers.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a polite number is a positive integer that can be written as the sum of two or more consecutive positive integers. Other positive integers are impolite.
Polite numbers have also been called staircase numbers because the Young diagrams representing graphically the partition
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
s of a polite number into consecutive integers (in the French style of drawing these diagrams) resemble staircases. If all numbers in the sum are strictly greater than one, the numbers so formed are also called trapezoidal numbers because they represent patterns of points arranged in a trapezoid
Trapezoid
In Euclidean geometry, a convex quadrilateral with one pair of parallel sides is referred to as a trapezoid in American English and as a trapezium in English outside North America. A trapezoid with vertices ABCD is denoted...
.
The problem of representing numbers as sums of consecutive integers and of counting the number of representations of this type has been studied by Sylvester
James Joseph Sylvester
James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...
, Mason, and Leveque
William J. LeVeque
William Judson LeVeque was an American mathematician and administrator who worked primarily in number theory. He was executive director of the American Mathematical Society during the 1970s and 1980s when that organization was growing rapidly and greatly increasing its use of computers in academic...
, as well as by many other more recent authors.
Examples and characterization
The first few polite numbers are- 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, ... .
The impolite numbers are exactly the powers of two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
. It follows from the Lambek–Moser theorem that the nth polite number is ƒ(n + 1), where
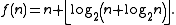
Politeness
The politeness of a positive number is defined as the number of ways it can be expressed as the sum of consecutive integers. For every x, the politeness of x equals the number of odd divisorDivisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s of x that are greater than one.
The politeness of the numbers 1, 2, 3, ... is
- 0, 0, 1, 0, 1, 1, 1, 0, 2, 1, 1, 1, 1, 1, 3, 0, 1, 2, 1, 1, 3, ... .
For instance, the politeness of 9 is 2 because it has two odd divisors, 3 and itself, and two polite representations
- 9 = 2 + 3 + 4 = 4 + 5;
the politeness of 15 is 3 because it has three odd divisors, 3, 5, and 15, and (as is familiar to cribbage
Cribbage
Cribbage, or crib, is a card game traditionally for two players, but commonly played with three, four or more, that involves playing and grouping cards in combinations which gain points...
players) three polite representations
- 15 = 4 + 5 + 6 = 1 + 2 + 3 + 4 + 5 = 7 + 8.
Construction of polite representations from odd divisors
To see the connection between odd divisors and polite representations, suppose a number x has the odd divisor y > 1. Then y consecutive integers centered on x/y (so that their average value is x/y) have x as their sum: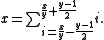
Some of the terms in this sum may be zero or negative. However, if a term is zero it can be omitted and any negative terms may be used to cancel positive ones, leading to a polite representation for x. (The requirement that y > 1 corresponds to the requirement that a polite representation have more than one term; applying the same construction for y = 1 would just lead to the trivial one-term representation x = x.)
For instance, the polite number x = 14 has a single nontrivial odd divisor, 7. It is therefore the sum of 7 consecutive numbers centered at 14/7 = 2:
- 14 = (2 − 3) + (2 − 2) + (2 − 1) + 2 + (2 + 1) + (2 + 2) + (2 + 3).
The first term, −1, cancels a later +1, and the second term, zero, can be omitted, leading to the polite representation
- 14 = 2 + (2 + 1) + (2 + 2) + (2 + 3) = 2 + 3 + 4 + 5.
Conversely, every polite representation of x can be formed from this construction. If a representation has an odd number of terms, x/y is the middle term, while if it has an even number of terms and its minimum value is m it may be extended in a unique way to a longer sequence with the same sum and an odd number of terms, by including the 2m − 1 numbers −(m − 1), −(m − 2), ..., −1, 0, 1, ..., −(m − 2), −(m − 1).
After this extension, again, x/y is the middle term. By this construction, the polite representations of a number and its odd divisors greater than one may be placed into a one-to-one correspondence
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
, giving a bijective proof
Bijective proof
In combinatorics, bijective proof is a proof technique that finds a bijective function f : A → B between two sets A and B, thus proving that they have the same number of elements, |A| = |B|. One place the technique is useful is where we wish to know the size of A, but can find no direct way of...
of the characterization of polite numbers and politeness. More generally, the same idea gives a two-to-one correspondence between, on the one hand, representations as a sum of consecutive integers (allowing zero, negative numbers, and single-term representations) and on the other hand odd divisors (including 1).
Another generalization of this result states that, for any n, the number of partitions of n into odd numbers having k distinct values equals the number of partitions of n into distinct numbers having k maximal runs of consecutive numbers.
Here a run is one or more consecutive values such that the next larger and the next smaller consecutive values are not part of the partition; for instance the partition 10 = 1 + 4 + 5 has two runs, 1 and 4 + 5.
A polite representation has a single run, and a partition with one value d is equivalent to a factorization of n as the product d×(n/d), so the special case k = 1 of this result states again the equivalence between polite representations and odd factors (including in this case the trivial representation n = n and the trivial odd factor 1).
Trapezoidal numbers
If a polite representation starts with 1, the number so represented is a triangular numberTriangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
Otherwise, it is the difference of two triangular numbers:
In the latter case, it is called a trapezoidal number. That is, a trapezoidal number is a polite number that has a polite representation in which all terms are strictly greater than one. The only polite numbers that may be non-trapezoidal are the triangular numbers with only one nontrivial odd divisor, because for those numbers, according to the bijection described earlier, the odd divisor corresponds to the triangular representation and there can be no other polite representations. Thus, polite non-trapezoidal numbers must have the form of a power of two multiplied by a prime number. As Jones and Lord observe, there are exactly two types of triangular numbers with this form:
- the even perfect numberPerfect numberIn number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
s 2n − 1(2n − 1) formed by the product of a Mersenne primeMersenne primeIn mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
2n − 1 with half the nearest power of twoPower of twoIn mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
, and - the products 2n − 1(2n + 1) of a Fermat prime 2n + 1 with half the nearest power of two.
For instance, the perfect number 28 = 23 − 1(23 − 1) and the number 136 = 24 − 1(24 + 1) are both polite triangular numbers that are not trapezoidal. It is believed that there are finitely many Fermat primes (only five of which — 3, 5, 17, 257, and 65,537 — have been discovered), but infinitely many Mersenne primes, in which case there are also infinitely many polite non-trapezoidal numbers.
External links
- An Introduction to Runsums, R. Knott.
- Is there any pattern to the set of trapezoidal numbers? Intellectualism.org question of the day, October 2, 2003. With a diagram showing trapezoidal numbers color-coded by the number of terms in their expansions.