Poly-Bernoulli number
Encyclopedia
In mathematics
, poly-Bernoulli numbers, denoted as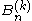
, were defined by M. Kaneko as
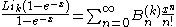
where Li is the polylogarithm. The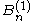
are the usual Bernoulli number
s.
Kaneko also gave two combinatorial formulas:
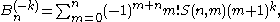
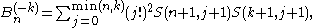
where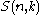
is the number of ways to partition a size 
set into 
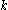non-empty subsets (the Stirling number of the second kind).
A combinatorial interpretation is that the poly-Bernoulli numbers of negative index enumerate the set of
by 
(0,1)-matrices uniquely reconstructible from their row and column sums.
For a positive integer n and a prime number p, the poly-Bernoulli numbers satisfy
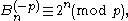
which can be seen as an analog of Fermat's little theorem
. Further, the equation
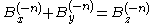
has no solution for integers x, y, z, n > 2; an analog of Fermat's last theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, poly-Bernoulli numbers, denoted as
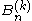, were defined by M. Kaneko as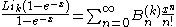where Li is the polylogarithm. The
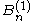are the usual Bernoulli numberBernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s.
Kaneko also gave two combinatorial formulas:
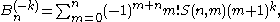
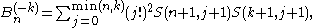
where
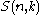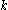is the number of ways to partition a size set into non-empty subsets (the Stirling number of the second kind).A combinatorial interpretation is that the poly-Bernoulli numbers of negative index enumerate the set of
by (0,1)-matrices uniquely reconstructible from their row and column sums.For a positive integer n and a prime number p, the poly-Bernoulli numbers satisfy
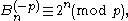
which can be seen as an analog of Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
. Further, the equation
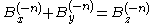
has no solution for integers x, y, z, n > 2; an analog of Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
.