Polynomial-time algorithm for approximating the volume of convex bodies
Encyclopedia
The paper
is a joint work by Martin Dyer
, Alan M. Frieze
and Ravindran Kannan
.
The main result of the paper is a randomized algorithm for finding an
approximation to the volume of a convex body 
in 
-dimensional Euclidean space by assume the existence of a membership oracle. The algorithm takes time bounded by a polynomial in 
, the dimension of 
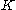and 
.
The algorithm is a sophisticated usage of the so-called Markov chain Monte Carlo
(MCMC) method.
The basic scheme of the algorithm is a nearly uniform sampling from within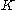
by placing a grid consisting 
-dimensional cubes and doing a random walk
over these cubes. By using the theory of
rapidly mixing Markov chains
, they show that it takes a polynomial time for the random walk to settle down to being a nearly uniform distribution.
is a joint work by Martin Dyer
Martin Dyer
Martin Edward Dyer is a professor in the School of Computing at the University of Leeds, Leeds, England. He graduated from the University of Leeds in 1967, obtained his MSc from Imperial College, University of London in 1968 and his PhD from the University of Leeds in 1979...
, Alan M. Frieze
Alan M. Frieze
Alan M. Frieze is a professor in the Department of Mathematical Sciences at Carnegie Mellon University, Pittsburgh, United States. He graduated from the University of Oxford in 1966, and obtained his PhD from the University of London in 1975. His research interests lie in combinatorics, discrete...
and Ravindran Kannan
Ravindran Kannan
Ravindran Kannan is currently a Principal Researcher at Microsoft Research India, where he leads the algorithms research group. He is also the first adjunct faculty of Computer Science and Automation Department of Indian Institute of Science. Before joining Microsoft, he was the William K. Lanman...
.
The main result of the paper is a randomized algorithm for finding an
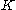approximation to the volume of a convex body in -dimensional Euclidean space by assume the existence of a membership oracle. The algorithm takes time bounded by a polynomial in , the dimension of and .The algorithm is a sophisticated usage of the so-called Markov chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
(MCMC) method.
The basic scheme of the algorithm is a nearly uniform sampling from within
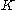by placing a grid consisting -dimensional cubes and doing a random walkRandom walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
over these cubes. By using the theory of
rapidly mixing Markov chains
Markov chain mixing time
In probability theory, the mixing time of a Markov chain is the time until the Markov chain is "close" to its steady state distribution.More precisely, a fundamental result about Markov chains is that a finite state irreducible aperiodic chain has a unique stationary distribution π and,...
, they show that it takes a polynomial time for the random walk to settle down to being a nearly uniform distribution.