
Polynomial matrix
Encyclopedia
A polynomial matrix or sometimes matrix polynomial is a matrix
whose elements are univariate or multivariate polynomial
s. A λ-matrix is a matrix whose elements are polynomials in λ.
A univariate polynomial matrix P of degree p is defined as:
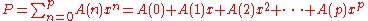
where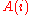 denotes a matrix of constant coefficients, and
denotes a matrix of constant coefficients, and  is non-zero. Thus a polynomial matrix is the matrix-equivalent of a polynomial, with each element of the matrix satisfying the definition of a polynomial of degree p.
is non-zero. Thus a polynomial matrix is the matrix-equivalent of a polynomial, with each element of the matrix satisfying the definition of a polynomial of degree p.
An example 3×3 polynomial matrix, degree 2:
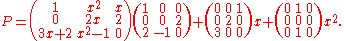
We can express this by saying that for a ring R, the rings and
and
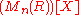 are isomorphic
are isomorphic
.
Note that polynomial matrices are not to be confused with monomial matrices, which are simply matrices with exactly one non-zero entry in each row and column.
If by λ we denote any element of the field
over which we constructed the matrix, by I the identity matrix, and we let A be a polynomial matrix, then the matrix λI-A is the characteristic matrix of the matrix A. Its determinant, |λI-A| is the characteristic polynomial
of the matrix A.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
whose elements are univariate or multivariate polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s. A λ-matrix is a matrix whose elements are polynomials in λ.
A univariate polynomial matrix P of degree p is defined as:
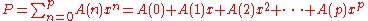
where
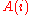 denotes a matrix of constant coefficients, and
denotes a matrix of constant coefficients, and  is non-zero. Thus a polynomial matrix is the matrix-equivalent of a polynomial, with each element of the matrix satisfying the definition of a polynomial of degree p.
is non-zero. Thus a polynomial matrix is the matrix-equivalent of a polynomial, with each element of the matrix satisfying the definition of a polynomial of degree p.An example 3×3 polynomial matrix, degree 2:
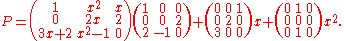
We can express this by saying that for a ring R, the rings
 and
and are isomorphic
are isomorphicRing homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
.
Properties
- A polynomial matrix over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
with determinant equal to a non-zero element of that field is called unimodularUnimodular matrixIn mathematics, a unimodular matrix M is a square integer matrix with determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N which is its inverse...
, and has an inverse that is also a polynomial matrix. Note that the only scalar unimodular polynomials are polynomials of degree 0 - nonzero constants, because an inverse of an arbitrary polynomial of higher degree is a rational function. - The roots of a polynomial matrix over the complex numbers are the points in the complex plane where the matrix loses rankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
.
Note that polynomial matrices are not to be confused with monomial matrices, which are simply matrices with exactly one non-zero entry in each row and column.
If by λ we denote any element of the field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
over which we constructed the matrix, by I the identity matrix, and we let A be a polynomial matrix, then the matrix λI-A is the characteristic matrix of the matrix A. Its determinant, |λI-A| is the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the matrix A.

