
Polytope model
Encyclopedia
The polyhedral model is a mathematical framework for loop nest optimization
in program optimization. The polytope method treats each loop iteration within nested loops as lattice points inside mathematical objects called polytope
s, performs affine transformation
s or more general non-affine transformations such as tiling on the polytopes, and then converts the transformed polytopes into equivalent, but optimized (depending on targeted optimization goal), loop nests through polyhedra scanning.
 The following C
The following C
code implements a form of error-distribution dither
ing similar to Floyd–Steinberg dithering, but modified for pedagogical reasons. The two-dimensional array
value between 0 and 255 inclusive. After the routine has finished, the output array
Each iteration of the inner loop
modifies the values in
 Performing the affine transformation
Performing the affine transformation 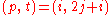 on the original dependency diagram gives us a new diagram, which is shown in the next image. We can then rewrite the code to loop on
on the original dependency diagram gives us a new diagram, which is shown in the next image. We can then rewrite the code to loop on
Loop nest optimization
Loop nest optimization applies a set of loop transformations for the purpose of locality optimization or parallelization or other loop overhead reduction of the loop nests...
in program optimization. The polytope method treats each loop iteration within nested loops as lattice points inside mathematical objects called polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s, performs affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s or more general non-affine transformations such as tiling on the polytopes, and then converts the transformed polytopes into equivalent, but optimized (depending on targeted optimization goal), loop nests through polyhedra scanning.
Detailed example

C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
code implements a form of error-distribution dither
Dither
Dither is an intentionally applied form of noise used to randomize quantization error, preventing large-scale patterns such as color banding in images...
ing similar to Floyd–Steinberg dithering, but modified for pedagogical reasons. The two-dimensional array
src contains h rows of w pixels, each pixel having a grayscaleGrayscale
In photography and computing, a grayscale or greyscale digital image is an image in which the value of each pixel is a single sample, that is, it carries only intensity information...
value between 0 and 255 inclusive. After the routine has finished, the output array
dst will contain only pixels with value 0 or value 255. During the computation, each pixel's dithering error is collected by adding it back into the src array. (Notice that src and dst are both read and written during the computation; src is not read-only, and dst is not write-only.)Each iteration of the inner loop
Inner loop
In computer programs, an important form of control flow is the loop. For example, this small pseudo-code program uses two nested loops to iterate over all the entries of an n×n matrix, changing their values so that the matrix becomes an identity matrix: for a in 1..n for b in 1..n ...
modifies the values in
src[i][j] based on the values of src[i-1][j], src[i][j-1], and src[i+1][j-1]. (The same dependencies apply to dst[i][j]. For the purposes of loop skewing, we can think of src[i][j] and dst[i][j] as the same element.) We can illustrate the dependencies of src[i][j] graphically, as in the diagram on the right.#define ERR(x,y) (dst[x][y] - src[x][y]) void dither(unsigned char **src, unsigned char **dst, int w, int h) { int i, j; for (j = 0; j < h; ++j) { for (i = 0; i < w; ++i) { int v = src[i][j]; if (i > 0) v -= ERR(i - 1, j) /2; if (j > 0) v -= ERR(i, j - 1) / 4; if (j > 0 && i < w - 1) v -= ERR(i + 1, j - 1) / 4; dst[i][j] = (v < 128) ? 0 : 255; src[i][j] = (v < 0) ? 0 : (v < 255) ? v : 255; } } } |

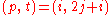 on the original dependency diagram gives us a new diagram, which is shown in the next image. We can then rewrite the code to loop on
on the original dependency diagram gives us a new diagram, which is shown in the next image. We can then rewrite the code to loop on p and t instead of i and j, obtaining the following "skewed" routine.void dither_skewed(unsigned char **src, unsigned char **dst, int w, int h) { int t, p; for (t = 0; t < (w + (2 * h)); ++t) { int pmin = max(t % 2, t - (2 * h) + 2); int pmax = min(t, w - 1); for (p = pmin; p <= pmax; p += 2) { int i = p; int j = (t - p) / 2; int v = src[i][j]; if (i > 0) v -= ERR(i - 1, j) / 2; if (j > 0) v -= ERR(i, j - 1) / 4; if (j > 0 && i < w - 1) v -= ERR(i + 1, j - 1) / 4; dst[i][j] = (v < 128) ? 0 : 255; src[i][j] = (v < 0) ? 0 : (v < 255) ? v : 255; } } } |
See also
- Frameworks supporting the polyhedral modelFrameworks supporting the polyhedral modelUse of the polyhedral model within a compiler requires software to represent the objects of this framework and perform operations upon them ....
- Loop nest optimizationLoop nest optimizationLoop nest optimization applies a set of loop transformations for the purpose of locality optimization or parallelization or other loop overhead reduction of the loop nests...
- Loop unrolling
- Loop reversal
- Loop tilingLoop tilingLoop tiling, also known as loop blocking, or strip mine and interchange, is a loop optimization used by compilers to make the execution of certain types of loops more efficient.- Overview :...
External links and references
- "The basic polytope method", tutorial by Martin Griebl containing diagrams of the pseudocode example above
- "Framework for polyhedral model"
- "Code Generation in the Polytope Model" (1998). Martin Griebl, Christian Lengauer, and Sabine Wetzel
- "The CLooG Polyhedral Code Generator"
- "CodeGen+: Z-polyhedra scanning"

