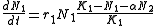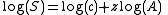Population modeling
Encyclopedia
A population model is a type of mathematical model
that is applied to the study of population dynamics.
Model
s allow a better understanding of how complex interactions and processes work. Modeling of dynamic interactions in nature can provide a manageable way of understanding how numbers change over time or in relation to each other. Ecological population modeling is concerned with the changes in population size and age distribution within a population as a consequence of interactions of organisms with the physical environment, with individuals of their own species, and with organisms of other species. The world is full of interactions that range from simple to dynamic. Many, if not all, of Earth’s processes affect human life. The Earth’s processes are greatly stochastic
and seem chaotic to the naked eye. However, a plethora of patterns can be noticed and are brought forth by using population modeling as a tool. Population models are used to determine maximum harvest for agriculturists, to understand the dynamics of biological invasions, and have numerous environmental conservation implications. Population models are also used to understand the spread of parasites, viruses, and disease. The realization of our dependence on environmental health has created a need to understand the dynamic interactions of the earth’s flora
and fauna
. Methods in population modeling have greatly improved our understanding of ecology and the natural world.
was one of the first to note that populations grew with a geometric pattern while contemplating the fate of humankind. One of the most basic and milestone models of population growth was the Logistic model of population growth formulated by Pierre François Verhulst
in 1838. The logistic model takes the shape of a sigmoid curve and describes the growth of a population as exponential, followed by a decrease in growth, and bound by a carrying capacity due to environmental pressures. Population modeling became of particular interest to biologists in the 20th century as pressure on limited means of sustenance due to increasing human populations in parts of Europe were noticed by biologist like Raymond Pearl
. In 1921 Pearl invited physicist A.J. Lotka to assist him in his lab. Lotka developed paired differential equations that showed the effect of a parasite on its prey. Mathematician Vito Volterra equated the relationship between two species independent from Lotka. Together, Lotka and Volterra formed the Lotka–Volterra model for competition that applies the logistic equation to two species illustrating competition, predation, and parasitism interactions between species. In 1939 contributions to population modeling were given by Patrick Leslie as he began work in biomathematics. Leslie emphasized the importance of constructing a life table in order to understand the effect that key life history strategies played in the dynamics of whole populations. Matrix algebra was used by Leslie in conjunction with life tables to extend the work of Lotka. Matrix models of populations calculate the growth of a population with life history variables. Later, Robert MacArthur and Edward Wilson characterized island biogeography. The Equilibrium Model of Island Biogeography describes the number of species on an island as equilibrium of immigration and extinction. The Logistic population model, the Lotka–Volterra model of community ecology, life table Matrix Modeling, the Equilibrium Model of Island Biogeography and variations thereof are the basis for ecological population modeling today.
Lotka-Volterra equation
:
Island biogeography
:
Species area:
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
that is applied to the study of population dynamics.
Model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
s allow a better understanding of how complex interactions and processes work. Modeling of dynamic interactions in nature can provide a manageable way of understanding how numbers change over time or in relation to each other. Ecological population modeling is concerned with the changes in population size and age distribution within a population as a consequence of interactions of organisms with the physical environment, with individuals of their own species, and with organisms of other species. The world is full of interactions that range from simple to dynamic. Many, if not all, of Earth’s processes affect human life. The Earth’s processes are greatly stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
and seem chaotic to the naked eye. However, a plethora of patterns can be noticed and are brought forth by using population modeling as a tool. Population models are used to determine maximum harvest for agriculturists, to understand the dynamics of biological invasions, and have numerous environmental conservation implications. Population models are also used to understand the spread of parasites, viruses, and disease. The realization of our dependence on environmental health has created a need to understand the dynamic interactions of the earth’s flora
Flora
Flora is the plant life occurring in a particular region or time, generally the naturally occurring or indigenous—native plant life. The corresponding term for animals is fauna.-Etymology:...
and fauna
Fauna
Fauna or faunæ is all of the animal life of any particular region or time. The corresponding term for plants is flora.Zoologists and paleontologists use fauna to refer to a typical collection of animals found in a specific time or place, e.g. the "Sonoran Desert fauna" or the "Burgess shale fauna"...
. Methods in population modeling have greatly improved our understanding of ecology and the natural world.
History
Late 18th-century biologists began to develop techniques in population modeling in order to understand dynamics of growing and shrinking populations of living organisms. Thomas MalthusThomas Malthus
The Reverend Thomas Robert Malthus FRS was an English scholar, influential in political economy and demography. Malthus popularized the economic theory of rent....
was one of the first to note that populations grew with a geometric pattern while contemplating the fate of humankind. One of the most basic and milestone models of population growth was the Logistic model of population growth formulated by Pierre François Verhulst
Pierre François Verhulst
Pierre François Verhulst was a mathematician and a doctor in number theory from the University of Ghent in 1825...
in 1838. The logistic model takes the shape of a sigmoid curve and describes the growth of a population as exponential, followed by a decrease in growth, and bound by a carrying capacity due to environmental pressures. Population modeling became of particular interest to biologists in the 20th century as pressure on limited means of sustenance due to increasing human populations in parts of Europe were noticed by biologist like Raymond Pearl
Raymond Pearl
Raymond Pearl was an American biologist, regarded as one of the founders of biogerontology. He spent most of his career at Johns Hopkins University in Baltimore....
. In 1921 Pearl invited physicist A.J. Lotka to assist him in his lab. Lotka developed paired differential equations that showed the effect of a parasite on its prey. Mathematician Vito Volterra equated the relationship between two species independent from Lotka. Together, Lotka and Volterra formed the Lotka–Volterra model for competition that applies the logistic equation to two species illustrating competition, predation, and parasitism interactions between species. In 1939 contributions to population modeling were given by Patrick Leslie as he began work in biomathematics. Leslie emphasized the importance of constructing a life table in order to understand the effect that key life history strategies played in the dynamics of whole populations. Matrix algebra was used by Leslie in conjunction with life tables to extend the work of Lotka. Matrix models of populations calculate the growth of a population with life history variables. Later, Robert MacArthur and Edward Wilson characterized island biogeography. The Equilibrium Model of Island Biogeography describes the number of species on an island as equilibrium of immigration and extinction. The Logistic population model, the Lotka–Volterra model of community ecology, life table Matrix Modeling, the Equilibrium Model of Island Biogeography and variations thereof are the basis for ecological population modeling today.
Equations
Logistic growth equation:Lotka-Volterra equation
Lotka-Volterra equation
The Lotka–Volterra equations, also known as the predator–prey equations, are a pair of first-order, non-linear, differential equations frequently used to describe the dynamics of biological systems in which two species interact, one a predator and one its prey...
:
Island biogeography
Island biogeography
Island biogeography is a field within biogeography that attempts to establish and explain the factors that affect the species richness of natural communities. The theory was developed to explain species richness of actual islands...
:
Species area:
See also
- Population dynamicsPopulation dynamicsPopulation dynamics is the branch of life sciences that studies short-term and long-term changes in the size and age composition of populations, and the biological and environmental processes influencing those changes...
- Population dynamics of fisheriesPopulation dynamics of fisheriesA fishery is an area with an associated fish or aquatic population which is harvested for its commercial or recreational value. Fisheries can be wild or farmed. Population dynamics describes the ways in which a given population grows and shrinks over time, as controlled by birth, death, and...
- Population ecologyPopulation ecologyPopulation ecology is a sub-field of ecology that deals with the dynamics of species populations and how these populations interact with the environment. It is the study of how the population sizes of species living together in groups change over time and space....
- Nurgaliev's lawNurgaliev's lawIn population dynamics, Nurgaliev's law is an equation that describes the rate of change of the size of a population at a given time, in terms of the current population size...
External links
- GreenBoxes code sharing network. Greenboxes (Beta) is a repository for open-source population modeling code. Greenboxes allows users an easy way to share their code and to search for others shared code.