Position-specific scoring matrix
Encyclopedia
A position weight matrix (PWM), also called position-specific weight matrix (PSWM) or position-specific scoring matrix (PSSM), is a commonly used representation of motifs
(patterns) in biological sequences.
A PWM is a matrix of score values that gives a weighted match to any given substring
of fixed length. It has one row for each symbol of the alphabet, and one column for each position in the pattern. The score assigned by a PWM to a substring
is defined as 
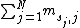, where 
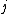represents position in the substring, 
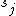is the symbol at position 
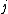in the substring, and 
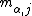is the score in row 
, column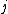 
of the matrix. In other words, a PWM score is the sum of position-specific scores for each symbol in the substring.
The score of a substring aligned with a PWM can be interpreted as the log-likelihood
of the substring under a product multinomial distribution. Since each column defines log-likelihoods for each of the different symbols, where the sum of likelihoods in a column equals one, the PWM corresponds to a Multinomial distribution. A PWM's score is the sum of log-likelihoods, which corresponds to the product of likelihoods, meaning that the score of a PWM is then a product-multinomial distribution. The PWM scores can also be interpreted in a physical framework as the sum of binding energies for all nucleotide
s (symbols of the substring) aligned with the PWM.
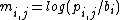, where 
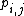is the probability of observing symbol i at position j of the motif, and 
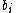is the probability of observing the symbol i in a background model. The PWM score then corresponds to the log-odds of the substring being generated by the motif versus being generated by the background, in a generative model
of the sequence.
(IC) of a PWM is sometimes of interest, as it says something about how different a given PWM is from a uniform distribution
.
The self-information
of observing a particular symbol at a particular position of the motif is: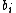
The expected (average) self-information of a particular element in the PWM is then: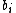
Finally, the IC of the PWM is then the sum of the expected self-information of every element:
Often, it is more useful to calculate the information content with the background letter frequencies of the sequences you are studying rather than assuming equal probabilities of each letter (e.g., the GC-content of DNA of thermophilic bacteria range from 65.3 to 70.8, thus a motif of ATAT would contain much more information than a motif of CCGG). The equation for information content thus becomes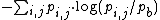
where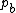
is the background frequency for that letter. This corresponds to the Kullback-Leibler divergence or relative entropy. However, it has been shown that when using PSSM to search genomic sequences (see below) this uniform correction can lead to overestimation of the importance of the different bases in a motif, due to the uneven distribution of n-mers in real genomes, leading to a significantly larger number of false positives.
Sequence motif
In genetics, a sequence motif is a nucleotide or amino-acid sequence pattern that is widespread and has, or is conjectured to have, a biological significance...
(patterns) in biological sequences.
A PWM is a matrix of score values that gives a weighted match to any given substring
Substring
A subsequence, substring, prefix or suffix of a string is a subset of the symbols in a string, where the order of the elements is preserved...
of fixed length. It has one row for each symbol of the alphabet, and one column for each position in the pattern. The score assigned by a PWM to a substring
Substring
A subsequence, substring, prefix or suffix of a string is a subset of the symbols in a string, where the order of the elements is preserved...
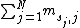is defined as , where 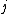represents position in the substring, 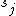is the symbol at position 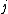in the substring, and 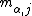is the score in row , column 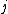of the matrix. In other words, a PWM score is the sum of position-specific scores for each symbol in the substring.Basic PWM with log-likelihoods
A PWM assumes independence between positions in the pattern, as it calculates scores at each position independently from the symbols at other positions.The score of a substring aligned with a PWM can be interpreted as the log-likelihood
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
of the substring under a product multinomial distribution. Since each column defines log-likelihoods for each of the different symbols, where the sum of likelihoods in a column equals one, the PWM corresponds to a Multinomial distribution. A PWM's score is the sum of log-likelihoods, which corresponds to the product of likelihoods, meaning that the score of a PWM is then a product-multinomial distribution. The PWM scores can also be interpreted in a physical framework as the sum of binding energies for all nucleotide
Nucleotide
Nucleotides are molecules that, when joined together, make up the structural units of RNA and DNA. In addition, nucleotides participate in cellular signaling , and are incorporated into important cofactors of enzymatic reactions...
s (symbols of the substring) aligned with the PWM.
Incorporating background distribution
Instead of using log-likelihood values in the PWM, as described in the previous paragraph, several methods uses log-odds scores in the PWMs. An element in a PWM is then calculated as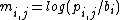, where 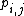is the probability of observing symbol i at position j of the motif, and 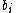is the probability of observing the symbol i in a background model. The PWM score then corresponds to the log-odds of the substring being generated by the motif versus being generated by the background, in a generative modelGenerative model
In probability and statistics, a generative model is a model for randomly generating observable data, typically given some hidden parameters. It specifies a joint probability distribution over observation and label sequences...
of the sequence.
Information content of a PWM
The information contentInformation content
The term information content is used to refer the meaning of information as opposed to the form or carrier of the information. For example, the meaning that is conveyed in an expression or document, which can be distinguished from the sounds or symbols or codes and carrier that physically form the...
(IC) of a PWM is sometimes of interest, as it says something about how different a given PWM is from a uniform distribution
Uniform distribution
-Probability theory:* Discrete uniform distribution* Continuous uniform distribution-Other:* "Uniform distribution modulo 1", see Equidistributed sequence*Uniform distribution , a type of species distribution* Distribution of military uniforms...
.
The self-information
Self-information
In information theory, self-information is a measure of the information content associated with the outcome of a random variable. It is expressed in a unit of information, for example bits,nats,or...
of observing a particular symbol at a particular position of the motif is:
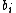
The expected (average) self-information of a particular element in the PWM is then:
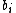
Finally, the IC of the PWM is then the sum of the expected self-information of every element:
Often, it is more useful to calculate the information content with the background letter frequencies of the sequences you are studying rather than assuming equal probabilities of each letter (e.g., the GC-content of DNA of thermophilic bacteria range from 65.3 to 70.8, thus a motif of ATAT would contain much more information than a motif of CCGG). The equation for information content thus becomes
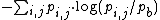
where
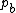is the background frequency for that letter. This corresponds to the Kullback-Leibler divergence or relative entropy. However, it has been shown that when using PSSM to search genomic sequences (see below) this uniform correction can lead to overestimation of the importance of the different bases in a motif, due to the uneven distribution of n-mers in real genomes, leading to a significantly larger number of false positives.