Positional game
Encyclopedia
Positional games are a class of combinatorial games. Well-known games that fall into this class include tic-tac-toe
, hex
and Shannon switching game
.
We say that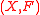
is a positional game, if 
is a finite set and 
is a collection of subsets of 
. We refer to 
as the board and 
as the winning sets. There are two players who alternately claim unclaimed elements of the board, until all the elements are claimed. Depending on the way the winner is determined, there are several versions of positional games.
The player who is first to claim all elements of one winning set wins. If the game is over (all elements of the board are claimed) and no player has claimed all elements of a winning set, it is a draw.
The players are called Maker and Breaker. Maker wins if he claims all elements of one winning set. Breaker wins otherwise, i.e., he wins if the game is over (all elements of the board are claimed), and Maker did not claim a whole winning set. Note that a draw is not possible.
The players are called Avoider and Enforcer. Enforcer wins if Avoider claims all elements of one winning set. Avoider wins otherwise, i.e., he wins if the game is over (all elements of the board are claimed), and he did not claim a whole winning set. Note that a draw is not possible.
Tic-tac-toe
Tic-tac-toe, also called wick wack woe and noughts and crosses , is a pencil-and-paper game for two players, X and O, who take turns marking the spaces in a 3×3 grid. The X player usually goes first...
, hex
Hex (board game)
Hex is a board game played on a hexagonal grid, theoretically of any size and several possible shapes, but traditionally as an 11x11 rhombus. Other popular dimensions are 13x13 and 19x19 as a result of the game's relationship to the older game of Go...
and Shannon switching game
Shannon switching game
The Shannon switching game is an abstract strategy game for two players, invented by Claude Shannon, and independently invented by David Gale; it has also been known as Gale, Bridg-It, and Bird Cage....
.
We say that
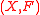is a positional game, if is a finite set and is a collection of subsets of . We refer to as the board and as the winning sets. There are two players who alternately claim unclaimed elements of the board, until all the elements are claimed. Depending on the way the winner is determined, there are several versions of positional games.- Strong games
The player who is first to claim all elements of one winning set wins. If the game is over (all elements of the board are claimed) and no player has claimed all elements of a winning set, it is a draw.
- Maker-Breaker gameMaker-Breaker gameMaker-Breaker games are a subclass of positional games.It is a two-person game with complete information played on a hypergraph where V is an arbitrary set and H is a family of subsets of V , called the winning sets...
s
The players are called Maker and Breaker. Maker wins if he claims all elements of one winning set. Breaker wins otherwise, i.e., he wins if the game is over (all elements of the board are claimed), and Maker did not claim a whole winning set. Note that a draw is not possible.
- Avoider-enforcer games
The players are called Avoider and Enforcer. Enforcer wins if Avoider claims all elements of one winning set. Avoider wins otherwise, i.e., he wins if the game is over (all elements of the board are claimed), and he did not claim a whole winning set. Note that a draw is not possible.