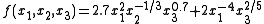Posynomial
Encyclopedia
A posynomial is a function
of the form
where all the coordinates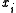 and coefficients
and coefficients 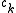 are positive real number
are positive real number
s, and the exponents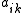 are real numbers. Posynomials are closed under addition, multiplication, and nonnegative scaling.
are real numbers. Posynomials are closed under addition, multiplication, and nonnegative scaling.
For example,
is a posynomial.
Posynomials are not the same as polynomial
s in several independent variables. A polynomial's exponents must be non-negative integers, but its independent variables and coefficients can be arbitrary real numbers; on the other hand, a posynomial's exponents can be arbitrary real numbers, but its independent variables and coefficients must be positive real numbers. This terminology was introduced by Richard J. Duffin, Elmor L. Peterson, and Clarence Zener in their seminal book on Geometric programming.
These functions are also known as "posinomials" in some literature.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the form
where all the coordinates
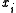 and coefficients
and coefficients 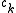 are positive real number
are positive real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, and the exponents
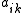 are real numbers. Posynomials are closed under addition, multiplication, and nonnegative scaling.
are real numbers. Posynomials are closed under addition, multiplication, and nonnegative scaling.For example,
is a posynomial.
Posynomials are not the same as polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in several independent variables. A polynomial's exponents must be non-negative integers, but its independent variables and coefficients can be arbitrary real numbers; on the other hand, a posynomial's exponents can be arbitrary real numbers, but its independent variables and coefficients must be positive real numbers. This terminology was introduced by Richard J. Duffin, Elmor L. Peterson, and Clarence Zener in their seminal book on Geometric programming.
These functions are also known as "posinomials" in some literature.
External links
- S. Boyd, S. J. Kim, L. Vandenberghe, and A. Hassibi, A Tutorial on Geometric Programming