Poynting's theorem
Encyclopedia
Poynting's theorem is a statement due to British physicist John Henry Poynting
about the conservation of energy
for the electromagnetic field
. Poynting's theorem takes into account the case when the electric and magnetic fields are coupled – static or stationary electric and magnetic fields are not coupled. In other words, Poynting theorem is valid only in electrodynamics. It relates the time derivative of the energy density, u to the energy flow and the rate at which the fields do work. It is summarised by the following formula:
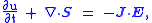
where S is the Poynting vector
representing the flow of energy, J is the current density
, E is the electric field
and u is the energy density defined by (symbol ε0 is the electric constant
and μ0 is the magnetic constant):
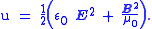
Since the magnetic field
does no work, the right hand side gives the negative of the total work done by the electromagnetic field per second·meter3.
Poynting's theorem in integral form:
where
is the surface which bounds (encloses) volume 
.
In electrical engineering context the theorem is usually written with the energy density term u expanded in the following way, which resembles the continuity equation
:
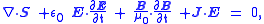
where
is the energy flow of the electromagnetic wave, 
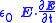is the density of reactive power
driving the build-up of electric field,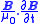
is the density of reactive power
driving the build-up of magnetic field, and
is the density of real power
dissipated by the Lorentz force
acting on charge carriers.
. First consider Faraday's Law
:
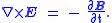
Taking the dot product
of this equation with
yields:
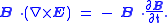
Next consider the Ampère-Maxwell law equation:
Taking the dot product of this equation with
yields: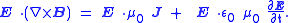
Subtracting the first dot product from the second yields: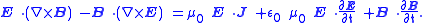
Finally, by the product rule
, as applied to the divergence
operator over the cross product
(described here):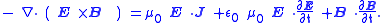
Since the Poynting vector
is defined as: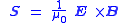
this is equivalent to: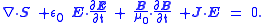
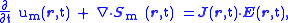
where u_m is the mechanical (kinetic) energy
density in the system. It can be described as the sum of kinetic energies of particles α (e.g., electrons in a wire), whose trajectory
is given by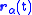
:
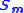is the flux of their energies, or a "mechanical Poynting vector":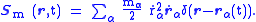
Both can be combined via the Lorentz force
, which the electromagnetical fields exert on the moving charged particles (see above), to the following energy continuity equation
or energy conservation law
:
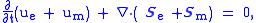
covering both types of energy and the conversion of one into the other.
as above, it is possible to follow the same style of derivation, but instead choose the Abraham form 
, the Minkowski form 
, or even the novel form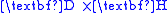 
. Each choice represents the response of the propagation medium in its own way: the 
form above has the elegant property of doing this with only electric currents, whilst the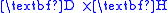 
form uses only (fictitious) magnetic monopole currents. The other two forms (Abraham and Minkowski) use complementary combinations of electric and magnetic currents to represent the polarization and magnetization responses of the medium.
John Henry Poynting
John Henry Poynting was an English physicist. He was a professor of physics at Mason Science College from 1880 until his death....
about the conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
for the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
. Poynting's theorem takes into account the case when the electric and magnetic fields are coupled – static or stationary electric and magnetic fields are not coupled. In other words, Poynting theorem is valid only in electrodynamics. It relates the time derivative of the energy density, u to the energy flow and the rate at which the fields do work. It is summarised by the following formula:
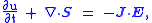
where S is the Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
representing the flow of energy, J is the current density
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
, E is the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and u is the energy density defined by (symbol ε0 is the electric constant
Electric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
and μ0 is the magnetic constant):
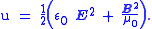
Since the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
does no work, the right hand side gives the negative of the total work done by the electromagnetic field per second·meter3.
Poynting's theorem in integral form:
where
is the surface which bounds (encloses) volume 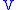.In electrical engineering context the theorem is usually written with the energy density term u expanded in the following way, which resembles the continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
:
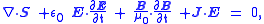
where
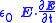is the energy flow of the electromagnetic wave, is the density of reactive powerElectric power
Electric power is the rate at which electric energy is transferred by an electric circuit. The SI unit of power is the watt.-Circuits:Electric power, like mechanical power, is represented by the letter P in electrical equations...
driving the build-up of electric field,
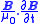is the density of reactive powerElectric power
Electric power is the rate at which electric energy is transferred by an electric circuit. The SI unit of power is the watt.-Circuits:Electric power, like mechanical power, is represented by the letter P in electrical equations...
driving the build-up of magnetic field, and
is the density of real powerElectric power
Electric power is the rate at which electric energy is transferred by an electric circuit. The SI unit of power is the watt.-Circuits:Electric power, like mechanical power, is represented by the letter P in electrical equations...
dissipated by the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
acting on charge carriers.
Derivation
The theorem can be derived from two of Maxwell's EquationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
. First consider Faraday's Law
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
:
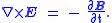
Taking the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of this equation with
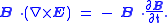
yields:Next consider the Ampère-Maxwell law equation:
Taking the dot product of this equation with
yields: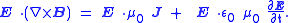Subtracting the first dot product from the second yields:
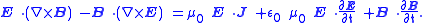
Finally, by the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
, as applied to the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
operator over the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
(described here):
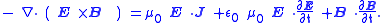
Since the Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
is defined as: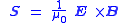this is equivalent to:
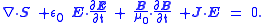
Generalization
The mechanical energy counterpart of the above theorem for the electromagnetical energy continuity equation is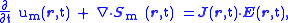where u_m is the mechanical (kinetic) energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
density in the system. It can be described as the sum of kinetic energies of particles α (e.g., electrons in a wire), whose trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
is given by
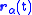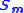: is the flux of their energies, or a "mechanical Poynting vector":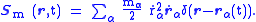Both can be combined via the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
, which the electromagnetical fields exert on the moving charged particles (see above), to the following energy continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
or energy conservation law
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
:
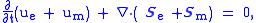
covering both types of energy and the conversion of one into the other.
Alternative forms
It is even possible to derive alternative versions of Poynting's theorem. Rather than using the flux vector as above, it is possible to follow the same style of derivation, but instead choose the Abraham form , the Minkowski form , or even the novel form 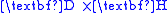. Each choice represents the response of the propagation medium in its own way: the form above has the elegant property of doing this with only electric currents, whilst the 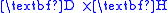form uses only (fictitious) magnetic monopole currents. The other two forms (Abraham and Minkowski) use complementary combinations of electric and magnetic currents to represent the polarization and magnetization responses of the medium.