
Prandtl–Glauert transformation
Encyclopedia
The Prandtl–Glauert transformation or Prandtl–Glauert rule (also Prandtl–Glauert–Ackeret rule) is an approximation function which allows comparison of aerodynamical processes occurring at different Mach number
s.
theory, can be multiplied with a correction factor to account for the influence of compressibility. The Prandtl–Glauert transformation is one such correction factor.
The Prandtl-Glauert transformation is found by linearizing the potential equations associated with compressible, inviscid flow. It was discovered that the linearized pressures in such a flow were equal to those found from incompressible flow theory multiplied by a correction factor. This correction factor is given below:
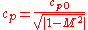
where
This correction factor works well for all Mach numbers 0.3 < M < 0.7
It should be noted that since this correction factor is derived from linearized equations, the calculated magnitude for the pressure is always less than the actual pressure within the fluid.
. The introduction of this relation allowed the design of aircraft which were able to operate in higher subsonic speed areas. Subsequently the equation was extended by Jakob Ackeret
to the common form used today, which is also valid in the supersonic region.
, although this point is not within the area of validity. The singularity is also called the Prandtl–Glauert singularity, and the flow resistance is calculated to approach infinity. In reality aerodynamic and thermodynamic perturbations get amplified strongly near the sonic speed, but a singularity does not occur. An explanation for this is that the Prandtl-Glauert transformation is a linearized approximation of compressible, inviscid potential flow. As the flow approaches sonic (M=1), the nonlinear phenomena dominate within the flow, which this transformation completely ignores for the sake of simplicity.
Despite this the theoretical singularity is often - however not correctly (see above) – used to explain phenomena near the sonic speed.
Mach number
Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure...
s.
Mathematical expression
In subsonic flow the compressibility of the fluid (often air) becomes more and more influential with increasing velocity. Thus, characteristic values of the flow, as found from incompressible, inviscid flowInviscid flow
In fluid dynamics there are problems that are easily solved by using the simplifying assumption of an ideal fluid that has no viscosity. The flow of a fluid that is assumed to have no viscosity is called inviscid flow....
theory, can be multiplied with a correction factor to account for the influence of compressibility. The Prandtl–Glauert transformation is one such correction factor.
The Prandtl-Glauert transformation is found by linearizing the potential equations associated with compressible, inviscid flow. It was discovered that the linearized pressures in such a flow were equal to those found from incompressible flow theory multiplied by a correction factor. This correction factor is given below:
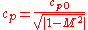
where
- cp is the compressible pressure coefficient
- cp0 is the incompressible pressure coefficient
- M is the Mach number.
This correction factor works well for all Mach numbers 0.3 < M < 0.7
It should be noted that since this correction factor is derived from linearized equations, the calculated magnitude for the pressure is always less than the actual pressure within the fluid.
Aerodynamic Coefficients
Since the aerodynamic coefficients of lift and drag are simply integrals of the pressure coefficient, the Prandtl-Glauert transformation is valid for these coefficients as well. The correction factor is not valid for wall shear stress or other viscous based interactions, however, as the correction is based on inviscid flow theory. This compressibility correction factor also affects lift slope curve for the lift coefficient with respect to angle of attack for aerodynamic structures.History
Ludwig Prandtl had been teaching this transformation in his lectures for a while, however the first publication was in 1928 by Hermann GlauertHermann Glauert
Hermann Glauert, FRS was a British aerodynamicist and Principal Scientific Officer of the Royal Aircraft Establishment, Farnborough until December 1934....
. The introduction of this relation allowed the design of aircraft which were able to operate in higher subsonic speed areas. Subsequently the equation was extended by Jakob Ackeret
Jakob Ackeret
Jakob Ackeret was a Swiss aeronautical engineer. He is widely viewed as one of the foremost aeronautics experts of 20th century.- Birth and education :...
to the common form used today, which is also valid in the supersonic region.
Singularity
Near the sonic speed (M=1) the transformation features a singularityMathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
, although this point is not within the area of validity. The singularity is also called the Prandtl–Glauert singularity, and the flow resistance is calculated to approach infinity. In reality aerodynamic and thermodynamic perturbations get amplified strongly near the sonic speed, but a singularity does not occur. An explanation for this is that the Prandtl-Glauert transformation is a linearized approximation of compressible, inviscid potential flow. As the flow approaches sonic (M=1), the nonlinear phenomena dominate within the flow, which this transformation completely ignores for the sake of simplicity.
Despite this the theoretical singularity is often - however not correctly (see above) – used to explain phenomena near the sonic speed.

