Price equation
Encyclopedia
The Price equation is a covariance
equation which is a mathematical description of evolution
and natural selection
. The Price equation was derived by George R. Price
, working in London to re-derive W.D. Hamilton's work on kin selection
. The Price equation also has applications in economics
.
Price's equation is a theorem
; it is a statement of mathematical fact between certain variables, and its value lies in the insight gained by assigning certain values encountered in evolutionary genetics to the variables. For example, it may be known that every pair of birds has two offspring. This can be encoded into the Price equation by saying that the fitness quantity of each individual has a value of 1, where "fitness" is defined to be the number of offspring from each individual. If it is also assumed that each offspring inherits the fitness of its parent, then:
These three points are mathematical facts following from knowledge of the fitness of every individual in one generation and how that fitness changes from parent to offspring. The Price equation provides the third bullet in more complicated situations where fitness may change from parent to offspring and certain individuals in a population may have a differential fitness advantage (i.e., individuals with certain traits will have more offspring than individuals with other traits). That is, the Price equation describes how the proportion of traits expressed in one generation changes over generational time. As the Price equation is a model of natural selection, it generally predicts that traits that yield a higher number of offspring than other traits will be favored in future generations.
 individuals over which the amount of a particular characteristic varies. Those
individuals over which the amount of a particular characteristic varies. Those  individuals can be grouped by the amount of the characteristic that each displays. In this case, at most there will be
individuals can be grouped by the amount of the characteristic that each displays. In this case, at most there will be  groups of
groups of  distinct values of the characteristic, and there will be at least 1 group of a single shared value of the characteristic. Index each group with
distinct values of the characteristic, and there will be at least 1 group of a single shared value of the characteristic. Index each group with 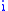 so that the number of members in the group is
so that the number of members in the group is 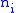 and the value of the characteristic shared among all members of the group is
and the value of the characteristic shared among all members of the group is 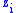 . Now assume that having
. Now assume that having 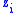 of the characteristic is associated with having a fitness
of the characteristic is associated with having a fitness
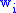 where the product
where the product  represents the number of offspring in the next generation. Denote this number of offspring from group
represents the number of offspring in the next generation. Denote this number of offspring from group 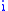 by
by 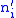 so that
so that 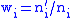 . Let
. Let 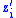 be the average
be the average
amount of the characteristic displayed by the offspring from group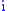 . Denote the amount of change in characteristic in group
. Denote the amount of change in characteristic in group 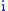 by
by 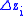 defined by
defined by
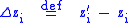
Now take to be the average characteristic value in this population and
to be the average characteristic value in this population and 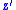 to be the average characteristic value in the next generation. Define the change in average characteristic by
to be the average characteristic value in the next generation. Define the change in average characteristic by  . That is,
. That is,
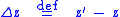
Note that this is not the average value of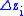 (as it is possible that
(as it is possible that  ). Also take
). Also take  to be the average fitness of this population. The Price equation states:
to be the average fitness of this population. The Price equation states:
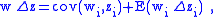
where the functions and
and  are respectively defined in Equations (1) and (2) below and are equivalent to the traditional definitions of sample mean and covariance; however, they are not meant to be statistical estimates of characteristics of a population. In particular, the Price equation is a deterministic difference equation that models the trajectory of of the actual mean value of a characteristic along the flow of an actual population of individuals. Assuming that the mean fitness
are respectively defined in Equations (1) and (2) below and are equivalent to the traditional definitions of sample mean and covariance; however, they are not meant to be statistical estimates of characteristics of a population. In particular, the Price equation is a deterministic difference equation that models the trajectory of of the actual mean value of a characteristic along the flow of an actual population of individuals. Assuming that the mean fitness  is not zero, it is often useful to write it as
is not zero, it is often useful to write it as
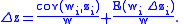
In the specific case that characteristic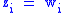 (i.e., fitness itself is the characteristic of interest), then Price's equation reformulates Fisher's fundamental theorem of natural selection
(i.e., fitness itself is the characteristic of interest), then Price's equation reformulates Fisher's fundamental theorem of natural selection
.
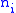 is the number of occurrences of a pair of real numbers
is the number of occurrences of a pair of real numbers 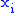 and
and 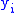 , then:
, then:
Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
equation which is a mathematical description of evolution
Evolution
Evolution is any change across successive generations in the heritable characteristics of biological populations. Evolutionary processes give rise to diversity at every level of biological organisation, including species, individual organisms and molecules such as DNA and proteins.Life on Earth...
and natural selection
Natural selection
Natural selection is the nonrandom process by which biologic traits become either more or less common in a population as a function of differential reproduction of their bearers. It is a key mechanism of evolution....
. The Price equation was derived by George R. Price
George R. Price
George Robert Price was an American population geneticist. Originally a physical chemist and later a science journalist, he moved to London in 1967, where he worked in theoretical biology at the Galton Laboratory, making three important contributions: first, rederiving W.D...
, working in London to re-derive W.D. Hamilton's work on kin selection
Kin selection
Kin selection refers to apparent strategies in evolution that favor the reproductive success of an organism's relatives, even at a cost to the organism's own survival and reproduction. Charles Darwin was the first to discuss the concept of group/kin selection...
. The Price equation also has applications in economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
.
Price's equation is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
; it is a statement of mathematical fact between certain variables, and its value lies in the insight gained by assigning certain values encountered in evolutionary genetics to the variables. For example, it may be known that every pair of birds has two offspring. This can be encoded into the Price equation by saying that the fitness quantity of each individual has a value of 1, where "fitness" is defined to be the number of offspring from each individual. If it is also assumed that each offspring inherits the fitness of its parent, then:
- Every individual in every generation of the population will have equal fitness.
- The population size will double from one generation to the next generation.
- Genes from an individual in one population will be equally represented in the next population. That is, the proportion of the population with those genes (e.g., 1/n for a population of n individuals) will be the same in subsequent generations (e.g., 2/(2n) for the population of 2n offspring).
These three points are mathematical facts following from knowledge of the fitness of every individual in one generation and how that fitness changes from parent to offspring. The Price equation provides the third bullet in more complicated situations where fitness may change from parent to offspring and certain individuals in a population may have a differential fitness advantage (i.e., individuals with certain traits will have more offspring than individuals with other traits). That is, the Price equation describes how the proportion of traits expressed in one generation changes over generational time. As the Price equation is a model of natural selection, it generally predicts that traits that yield a higher number of offspring than other traits will be favored in future generations.
Derivation
Suppose there is a population of individuals over which the amount of a particular characteristic varies. Those
individuals over which the amount of a particular characteristic varies. Those  individuals can be grouped by the amount of the characteristic that each displays. In this case, at most there will be
individuals can be grouped by the amount of the characteristic that each displays. In this case, at most there will be  groups of
groups of  distinct values of the characteristic, and there will be at least 1 group of a single shared value of the characteristic. Index each group with
distinct values of the characteristic, and there will be at least 1 group of a single shared value of the characteristic. Index each group with 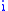 so that the number of members in the group is
so that the number of members in the group is 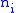 and the value of the characteristic shared among all members of the group is
and the value of the characteristic shared among all members of the group is 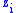 . Now assume that having
. Now assume that having 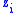 of the characteristic is associated with having a fitness
of the characteristic is associated with having a fitnessFitness (biology)
Fitness is a central idea in evolutionary theory. It can be defined either with respect to a genotype or to a phenotype in a given environment...
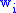 where the product
where the product  represents the number of offspring in the next generation. Denote this number of offspring from group
represents the number of offspring in the next generation. Denote this number of offspring from group 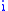 by
by 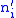 so that
so that 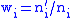 . Let
. Let 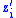 be the average
be the averageAverage
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
amount of the characteristic displayed by the offspring from group
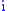 . Denote the amount of change in characteristic in group
. Denote the amount of change in characteristic in group 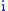 by
by 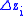 defined by
defined by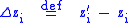
Now take
 to be the average characteristic value in this population and
to be the average characteristic value in this population and 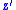 to be the average characteristic value in the next generation. Define the change in average characteristic by
to be the average characteristic value in the next generation. Define the change in average characteristic by  . That is,
. That is,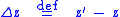
Note that this is not the average value of
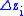 (as it is possible that
(as it is possible that  ). Also take
). Also take  to be the average fitness of this population. The Price equation states:
to be the average fitness of this population. The Price equation states: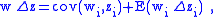
where the functions
 and
and  are respectively defined in Equations (1) and (2) below and are equivalent to the traditional definitions of sample mean and covariance; however, they are not meant to be statistical estimates of characteristics of a population. In particular, the Price equation is a deterministic difference equation that models the trajectory of of the actual mean value of a characteristic along the flow of an actual population of individuals. Assuming that the mean fitness
are respectively defined in Equations (1) and (2) below and are equivalent to the traditional definitions of sample mean and covariance; however, they are not meant to be statistical estimates of characteristics of a population. In particular, the Price equation is a deterministic difference equation that models the trajectory of of the actual mean value of a characteristic along the flow of an actual population of individuals. Assuming that the mean fitness  is not zero, it is often useful to write it as
is not zero, it is often useful to write it as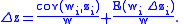
In the specific case that characteristic
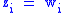 (i.e., fitness itself is the characteristic of interest), then Price's equation reformulates Fisher's fundamental theorem of natural selection
(i.e., fitness itself is the characteristic of interest), then Price's equation reformulates Fisher's fundamental theorem of natural selectionFisher's fundamental theorem of natural selection
In population genetics, R. A. Fisher's fundamental theorem of natural selection was originally stated as:Or, in more modern terminology:- History :...
.
Proof of the Price equation
To prove the Price equation, the following definitions are needed. If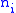 is the number of occurrences of a pair of real numbers
is the number of occurrences of a pair of real numbers 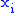 and
and 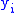 , then:
, then:- The mean of the
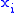 values is:
values is:

- The covariance between the
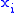 and
and 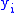 values is:
values is:
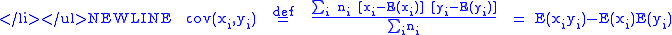
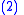
The notation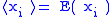 will also be used when
will also be used when
convenient.
Suppose there is a population of organisms all of which have a genetic characteristic described by some real number. For example, high values of the number represent an increased visual acuity over some other organism with a lower value of the characteristic. Groups can be defined in the population which are characterized by having the same value of the characteristic. Let subscript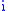 identify the group with characteristic
identify the group with characteristic 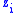 and let
and let 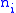 be the number of organisms in that group. The total number of organisms is then
be the number of organisms in that group. The total number of organisms is then  where:
where:
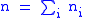
The average value of the characteristic is defined as:
defined as:
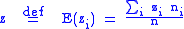
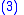
Now suppose that the population reproduces, all parents are eliminated, and then there is a selection process on the children, by which less fit children are removed from the reproducing population. After reproduction and selection, the population numbers for the child groups will change to n′i. Primes will be used to denote child parameters, unprimed variables denote parent parameters.
The total number of children is n' where:
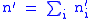
The fitness of group i will be defined to be the ratio of children to parents:
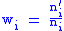
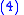
with average fitness of the population being
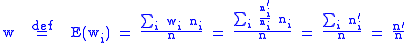
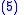
The average value of the child characteristic will be z' where:
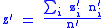
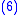
where z′i are the (possibly new) values of the characteristic in the child population. Equation (2) shows that:
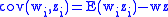
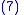
Call the change in characteristic value from parent to child populations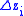 so that
so that 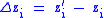 . As seen in Equation (1), the expected value operator
. As seen in Equation (1), the expected value operator  is linearLinearIn mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
is linearLinearIn mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, so
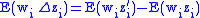
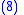
Combining Equations (7) and (8) leads to
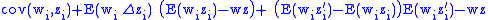
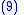
but from Equation (1) gives:
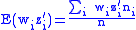
and from Equation (4) gives:
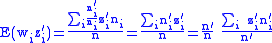
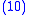
Applying Equations (5) and (6) to Equation (10) and then applying the result to Equation (9) gives the Price Equation:
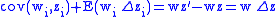
Simple Price equation
When the characters zi do not change from the parent to the child generation, the second term in the Price equation becomes zero resulting in a simplified version of the Price equation:
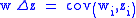
which can be restated as:
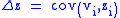
where vi is the fractional fitness: vi= wi/w.
This simple Price equation can be proven using the definition in Equation (2) above.
It makes this fundamental statement about
evolution: "If a certain inheritable characteristic is correlated with an increase in fractional fitness, the average value of that characteristic in the child population will be increased over that in the parent population."
Example: Evolution of sight
As an example of the simple Price equation, consider a model for the evolution of sight. Suppose
zi is a real number measuring the visual acuity of an organism. An organism with a higher zi will have better sight than one with a lower value of zi. Let us say that the fitness of such an organism is wi=zi which means the more sighted it is, the fitter it is, that is, the more children it will produce. Beginning with the following description of a parent population composed of 3 types: (i = 0,1,2) with sightedness values zi = 3,2,1:i 0 1 2 ni 10 20 30 zi 3 2 1
Using Equation (4), the
child population (assuming the character zi doesn't
change; that is, zi = zi')i 0 1 2 ni' 30 40 30 zi' 3 2 1
We would like to know how much average visual acuity has increased or decreased in the population. From Equation (3), the average sightedness of the parent population is z = 5/3. The average sightedness of the child population is z = 2, so that the change in average sightedness is:
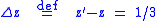
which indicates that the trait of sightedness is
increasing in the population. Applying the Price equation we
have (since z′i= zi):
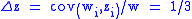
Dynamical sufficiency and the simple Price equation
Sometimes the genetic model being used encodes enough information into the parameters used by the Price equation to allow the calculation of the parameters for all subsequent generations. This property is referred to as dynamical sufficiency. For simplicity, the following looks at dynamical sufficiency for the simple Price equation, but is also valid for the full Price equation.
Referring to the definition in Equation (2), the simple Price equation for the character z can be written:
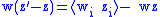
For the second generation:
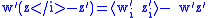
The simple Price equation for z only gives us the value of z ' for the first generation, but does not give us the value of w ' and ⟨w 'i z 'i ⟩ which are needed to calculate z″ for the second generation. The variables w ' and ⟨w 'i z 'i ⟩ can both be thought of characteristics of the first generation, so the Price equation can be used to calculate them as well:
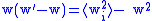
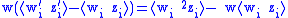
The five 0-generation variables w, z, ⟨wi zi ⟩, ⟨w2i ⟩, and ⟨w2i zi ⟩ which must be known before proceeding to calculate the three first generation variables w ', z ', and ⟨w 'i z 'i ⟩, which are needed to calculate z″ for the second generation. It can be seen that in general the Price equation cannot be used to propagate forward in time unless there is a way of calculating the higher moments (⟨wni ⟩ and ⟨wni zi ⟩) from the lower moments in a way that is independent of the generation. Dynamical sufficiency means that such equations can be found in the genetic model, allowing the Price equation to be used alone as a propagator of the dynamicsEvolutionary dynamicsEvolutionary dynamics is the study of the mathematical principles according to which life has evolved and continues to evolve. In this area, Evolution has become a mathematical theory, and any idea of an evolutionary process or mechanism should be studied in the context of the mathematical...
of the model forward in time.
Example: Evolution of sickle cell anemia
As an example of dynamical sufficiency, consider the case of sickle cell anemia.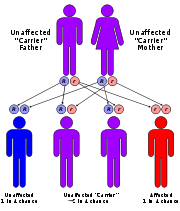
Each person has two sets of genes, one set inherited from the father, one from the mother. Sickle cell anemia is a blood disorder which occurs when a particular pair of genes both carry the 'sickle-cell trait'. The reason that the sickle-cell gene has not been eliminated from the human population by selection is because when there is only one of the pair of genes carrying the sickle-cell trait, that individual (a "carrier") is highly resistant to malaria, while a person who has neither gene carrying the sickle-cell trait will be susceptible to malaria. Let's see what the Price equation has to say about this.
Let zi=i be the number of sickle-cell genes that organisms of type
i have so that zi = 0 or 1 or 2. Assume the population sexually
reproduces and matings are random between type 0 and 1, so that the number of
0–1 matings is n0n1/(n0+n1) and the
number of i–i matings is n2i/[2(n0+n1)] where i = 0
or 1. Suppose also that each gene has a 1/2 chance of being passed to any given
child and that the initial population is
ni=[n0,n1,n2]. If b is the
birth rate, then after reproduction there will be
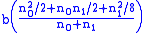 type 0 children (unaffected)
type 0 children (unaffected)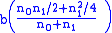 type 1 children (carriers)
type 1 children (carriers)
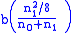 type 2 children (affected)
type 2 children (affected)
Suppose a fraction a of type 0 reproduce, the loss being due to malaria. Suppose all of type 1 reproduce, since they are resistant to malaria, while none of the type 2 reproduce, since they all have sickle-cell anemia. The fitness coefficients are then:
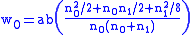
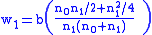
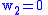
To find the concentration n1 of carriers in the population at equilibrium, with the equilibrium condition of Δ z=0, the simple Price equation is used:
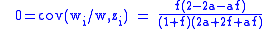
where f=n1/n0. At equilibrium then, assuming f is
not zero:
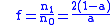
In other words the ratio of carriers to non-carriers will be equal to the above constant non-zero value. In the absence of malaria, a=1 and f=0 so that the sickle-cell gene is eliminated from the gene pool. For any presence of malaria, a will be smaller than unity and the sickle-cell gene will persist.
The situation has been effectively determined for the infinite (equilibrium) generation. This means that there is dynamical sufficiency with respect to the Price equation, and that there is an equation relating higher moments to lower moments. For example, for the second moments:
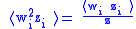
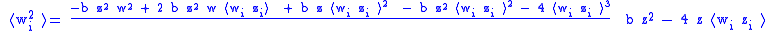
Example: sex ratios
In a 2-sex species or deme with sexes 1 and 2 where ,
,
 ,
,
 is the relative frequency of sex 1. Since all individuals have one parent of each sex, the fitness of each sex is proportional to the other sex's size. Consider proportionality constants
is the relative frequency of sex 1. Since all individuals have one parent of each sex, the fitness of each sex is proportional to the other sex's size. Consider proportionality constants 
and
such that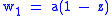
and .
.
This gives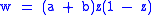
and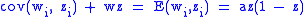 ,
,
so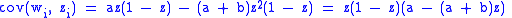 .
.
Hence,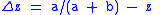
so that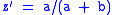 .
.
Full Price equation
The simple Price equation was based on the assumption that the characters
zi do not change over one generation. If it is assumed that they do change, with zi being the value of the character in the child population, then the full Price equation must be used. A change in character can come about in a number of ways. The following two examples illustrate two such possibilities, each of which introduces new insight into the Price equation.
Example: Evolution of altruism
To study the evolution of a genetic predisposition to altruism, altruism will be defined as the genetic predisposition to behavior which decreases individual fitness while increasing the average fitness of the group to which the individual belongs. First specifying a simple model, which will only require the simple Price equation. Specify a fitness wi by a model equation:
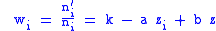
where zi is a measure of altruism, the azi term is the decrease in fitness of an individual due to altruism towards the group and bz is the increase in fitness of an individual due to the altruism of the group towards an individual.
Assume that a and b are both greater than zero. From the Price equation:
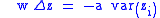
where var(zi) is the varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of zi which is just the covariance of zi with itself:
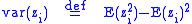
It can be seen that, by this model, in order for altruism to persist it must be uniform
throughout the group. If there are two altruist types the average altruism of the group will decrease, the more altruistic will lose out to the less altruistic.
Now assuming a hierarchy of groups which will require the full Price equation. The population will be divided into groups, labelled with index i and then each group will have a set of subgroups labelled by index j. Individuals will thus be identified by two indices,
i and j, specifying which group and subgroup they belong to. nij will
specify the number of individuals of type ij. Let zij be the degree of
altruism expressed by individual j of group i towards the members of group i. Let's specify the fitness wij by a model equation:
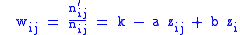
The a zij term is the fitness the organism loses by being altruistic and is
proportional to the degree of altruism zij that it expresses towards members
of its own group. The b zi term is the fitness that the organism gains from the altruism of the members of its group, and is proportional to the average altruism zi expressed by the group towards its members. Again, in studying altruistic (rather than spiteful) behavior, it is expected that a and b are positive numbers. Note that the above behavior is altruistic only when azij >bzi. Defining the group averages:
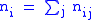
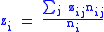
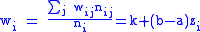
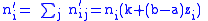
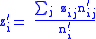
and global averages:
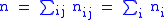
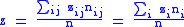
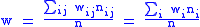
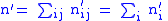
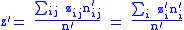
It can be seen that since the zi and zi are now averages over a particular group, and since these groups are subject to selection, the value of Δzi = z′i−zi will not necessarily be zero, and the full Price equation will be needed.
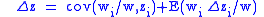
In this case, the first term isolates the advantage to each group conferred by having altruistic members. The second term isolates the loss of altruistic members from their group due to their altruistic behavior. The second term will be negative. In other words there will be an average loss of altruism due to the in-group loss of altruists, assuming that the altruism is not uniform across the group. The first term is:
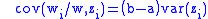
In other words, for b>a there may be a positive contribution to the average altruism as a result of a group growing due to its high number of altruists and this growth can offset in-group losses, especially if the variance of the in-group altruism is low. In order for this effect to be significant, there must be a spread in the average altruism of the groups.
Example: Evolution of mutability
Suppose there is an environment containing two kinds of food. Let α be the amount of the first kind of food and β be the amount of the second kind. Suppose an organism has a single allele which allows it to utilize a particular food. The allele has four gene forms: A0, Am, B0, and Bm. If an organism's single food gene is of the A type, then the organism can utilize A-food only, and its survival is proportional to α. Likewise, if an organism's single food gene is of the B type, then the organism can utilize B-food only, and its survival is proportional to β. A0 and Am are both A-alleles, but organisms with the A0 gene produce offspring with A0-genes
only, while organisms with the Am gene produce (1−3m) offspring with the Am gene, and m organisms of the remaining three gene types. Likewise, B0 and Bm are both B-alleles, but organisms with the B0 gene produce offspring with B0-genes only, while
organisms with the Bm gene produce (1−3m) offspring with the Bm gene, and m organisms of the remaining three gene types.
Let i=0,1,2,3 be the indices associated with the A0, Am, B0, and Bm genes respectively. Let wij be the number of viable type-j organisms produced per type-i organism. The wij matrix is: (with i denoting rows and j denoting columns)
α 0 0 0 mα (1−3m)α mβ mβ 0 0 β 0 mα mα mβ (1−3m)β
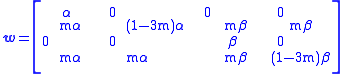
Mutators are at a disadvantage when the food supplies α and β are constant. They lose every generation compared to the non-mutating genes. But when the food supply varies, even though the mutators lose relative to an A or B non-mutator, they may lose less than them over the long run because, for example, an A type loses a lot when α is low. In this way, "purposeful" mutation may be selected for. This may explain the redundancy in the genetic code, in which some amino acidAmino acidAmino acids are molecules containing an amine group, a carboxylic acid group and a side-chain that varies between different amino acids. The key elements of an amino acid are carbon, hydrogen, oxygen, and nitrogen...
s are encoded by more than one codon in the DNADNADeoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
. Although the codons produce the same amino acids, they have an effect on the mutability of the DNA, which may be selected for or against under certain conditions.
With the introduction of mutability, the question of identity versus lineage arises. Is fitness measured by the number of children an individual has, regardless of the children's genetic makeup, or is fitness the child/parent ratio of a particular genotype?. Fitness is itself a characteristic, and as a result, the Price equation will handle both.
Suppose we want to examine the evolution of mutator genes. Define the z-score as:
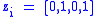
in other words, 0 for non-mutator genes, 1 for mutator genes. There are
two cases:
Genotype fitness
We focus on the idea of the fitness of the genotype. The index i indicates the genotype and the number of type i genotypes in the child population is: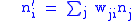
which gives fitness: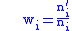
Since the individual mutability zi does not change, the average mutabilities will be:
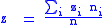
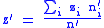
with these definitions, the simple Price equation now applies.
Lineage fitness
In this case we want to look at the idea that fitness is measured by the number of children an organism has, regardless of their genotype. Note that we now have two methods of grouping, by lineage, and by genotype. It is this complication that will introduce the need for the full Price equation. The number of children an i-type organism has is: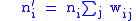
which gives fitness:
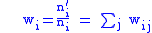
We now have characters in the child population which are the average character of the i-th parent.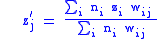
with global characters:
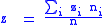
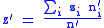
with these definitions, the full Price equation now applies.
Criticism on the use of the Price equation
A critical discussion of the use of the Price equation can be found in this website. The authors argue that the Price equation is an identity without predictive value.
Cultural references
Price's equation features in the plot and title of the 2008 thriller film WΔZ (http://www.imdb.com/title/tt0804552).
- The covariance between the

