
Prime decomposition (3-manifold)
Encyclopedia
In mathematics
, the prime decomposition theorem for 3-manifolds states that every compact
, orientable
3-manifold
is the connected sum
of a unique (up to
homeomorphism
) collection of prime 3-manifolds.
A manifold is prime if it cannot be presented as a connected sum in a non-trivial way, where the trivial way is
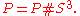
If P is a prime 3-manifold then either it is S2 × S1 or the non-orientable S2 bundle
over S1,
or any embedded 2-sphere in P bounds a ball, i.e. is irreducible. So the theorem can be restated to say that there is a unique connected sum decomposition into irreducible 3-manifolds and S2 × S1's.
The prime decomposition holds also for non-orientable 3-manifolds, but the uniqueness statement must be modified slightly: every compact, non-orientable 3-manifold is a connected sum of irreducible 3-manifolds and non-orientable S2 bundle
s over S1. This sum is unique as long as we specify that each summand is either irreducible or a non-orientable S2 bundle
over S1.
The proof is based on normal surface
techniques originated by Hellmuth Kneser
. Existence was proven by Kneser, but the exact formulation and proof of the uniqueness was done more than 30 years later by John Milnor
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the prime decomposition theorem for 3-manifolds states that every compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, orientable
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
is the connected sum
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
of a unique (up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
) collection of prime 3-manifolds.
A manifold is prime if it cannot be presented as a connected sum in a non-trivial way, where the trivial way is
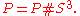
If P is a prime 3-manifold then either it is S2 × S1 or the non-orientable S2 bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
over S1,
or any embedded 2-sphere in P bounds a ball, i.e. is irreducible. So the theorem can be restated to say that there is a unique connected sum decomposition into irreducible 3-manifolds and S2 × S1's.
The prime decomposition holds also for non-orientable 3-manifolds, but the uniqueness statement must be modified slightly: every compact, non-orientable 3-manifold is a connected sum of irreducible 3-manifolds and non-orientable S2 bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s over S1. This sum is unique as long as we specify that each summand is either irreducible or a non-orientable S2 bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
over S1.
The proof is based on normal surface
Normal surface
In mathematics, a normal surface is a surface inside a triangulated 3-manifold that intersects each tetrahedron so that each component of intersection is a triangle or a quad . A triangle cuts off a vertex of the tetrahedron while a quad separates pairs of vertices...
techniques originated by Hellmuth Kneser
Hellmuth Kneser
Hellmuth Kneser was a German mathematician, who made notable contributions to group theory and topology. His most famous result may be his theorem on the existence of a prime decomposition for 3-manifolds...
. Existence was proven by Kneser, but the exact formulation and proof of the uniqueness was done more than 30 years later by John Milnor
John Milnor
John Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
.

