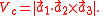Primitive cell
Encyclopedia
Used predominantly in geometry
, solid state physics, and mineralogy
, particularly in describing crystal structure
, a primitive cell is a minimum cell corresponding to a single lattice point of a structure with translational symmetry
in 2 dimensions, 3 dimensions, or other dimensions. A lattice can be characterized by the geometry of its primitive cell.
The primitive cell is a fundamental domain
with respect to translational symmetry only. In the case of additional symmetries a fundamental domain is smaller.
A crystal
can be categorized by its lattice and the atoms that lie in a primitive cell (the basis). A cell will fill all the lattice space without leaving gaps by repetition of crystal translation operations.
Primitive translation vectors are used to define a crystal translation vector,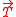
, and also gives a lattice cell of smallest volume for a particular lattice. The lattice and translation vectors 
, 
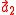, and 
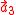are primitive if the atoms look the same from any lattice points using integers 
, 
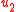, and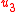 
.
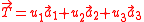
The primitive cell is defined by the primitive axes (vectors)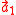
, 
, and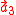 
. The volume, 
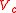, of the primitive cell is given by the parallelepiped
from the above axes as,
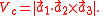
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, solid state physics, and mineralogy
Mineralogy
Mineralogy is the study of chemistry, crystal structure, and physical properties of minerals. Specific studies within mineralogy include the processes of mineral origin and formation, classification of minerals, their geographical distribution, as well as their utilization.-History:Early writing...
, particularly in describing crystal structure
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
, a primitive cell is a minimum cell corresponding to a single lattice point of a structure with translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
in 2 dimensions, 3 dimensions, or other dimensions. A lattice can be characterized by the geometry of its primitive cell.
The primitive cell is a fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
with respect to translational symmetry only. In the case of additional symmetries a fundamental domain is smaller.
A crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
can be categorized by its lattice and the atoms that lie in a primitive cell (the basis). A cell will fill all the lattice space without leaving gaps by repetition of crystal translation operations.
Primitive translation vectors are used to define a crystal translation vector,
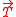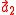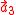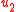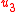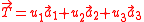
, and also gives a lattice cell of smallest volume for a particular lattice. The lattice and translation vectors , , and are primitive if the atoms look the same from any lattice points using integers , , and .The primitive cell is defined by the primitive axes (vectors)
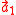, , and 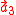. The volume, 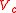, of the primitive cell is given by the parallelepipedParallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
from the above axes as,