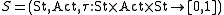Probabilistic bisimulation
Encyclopedia
In theoretical computer science
, probabilistic bisimulation is an extension of the concept of bisimulation
for fully probabilistic transition systems
first described by K.G. Larsen and A. Skou.
A discrete probabilistic transition system is a triple
where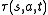
gives the probability of starting in the state s, performing the action a and ending up in the state t. The set of states is assumed to be countable. There is no attempt to assign probabilities to actions. It is assumed that the actions are chosen nondeterministically by an adversary or by the environment. This type of system is fully probabilistic, there is no other indeterminacy.
The definition of a probabilistic bisimulation on a system S is an equivalence relation R on the state space St, such that for every pair s,t in St with sRt and for every action a in Act and for every equivalence class C of R
Two states are said to be probabilistically bisimilar if there is some such R relating them.
When applied to Markov chains, probabilistic bisimulation is the same concept as lumpability
.
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
, probabilistic bisimulation is an extension of the concept of bisimulation
Bisimulation
In theoretical computer science a bisimulation is a binary relation between state transition systems, associating systems which behave in the same way in the sense that one system simulates the other and vice-versa....
for fully probabilistic transition systems
State transition system
In theoretical computer science, a state transition system is an abstract machine used in the study of computation. The machine consists of a set of states and transitions between states, which may be labeled with labels chosen from a set; the same label may appear on more than one transition...
first described by K.G. Larsen and A. Skou.
A discrete probabilistic transition system is a triple
where
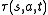gives the probability of starting in the state s, performing the action a and ending up in the state t. The set of states is assumed to be countable. There is no attempt to assign probabilities to actions. It is assumed that the actions are chosen nondeterministically by an adversary or by the environment. This type of system is fully probabilistic, there is no other indeterminacy.The definition of a probabilistic bisimulation on a system S is an equivalence relation R on the state space St, such that for every pair s,t in St with sRt and for every action a in Act and for every equivalence class C of R
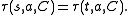Two states are said to be probabilistically bisimilar if there is some such R relating them.When applied to Markov chains, probabilistic bisimulation is the same concept as lumpability
Lumpability
In probability theory, lumpability is a method for reducing the size of the state space of some continuous-time Markov chains, first published by Kemeny and Snell.-Definition:...
.