
Probability plot
Encyclopedia
In statistics
, a P-P plot (probability-probability plot or percent-percent plot) is a probability plot
for assessing how closely two data set
s agree, which plots the two cumulative distribution function
s against each other.
The Q-Q plot
is more widely used, but they are both referred to as "the" probability plot, and are potentially confused.
s (cdfs) against each other:
given two probability distributions, with cdfs "F" and "G", it plots as z ranges from
as z ranges from 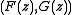 to
to  As a cdf has range [0,1], the domain of this parametric graph is
As a cdf has range [0,1], the domain of this parametric graph is 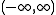 and the range is the unit square
and the range is the unit square 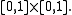
Thus for input z the output is the pair of numbers giving what percentage of f and what percentage of g fall at or below z.
The comparison line is the 45° line from (0,0) to (1,1) – the distributions are equal if and only if the plot falls on this line – any deviation indicates a difference between the distributions.
.
P-P plots are sometimes limited to comparisons between two samples, rather than comparison of a sample to a theoretical model distribution. However, they are of general use, particularly where observations are not all modelled with the same distribution.
However, it was found some use in comparing a sample distribution from a known theoretical distribution: given n samples, plotting the continuous theoretical cdf against the empirical cdf would yield a stair-step (a step as z hits a sample), and would hit the top of the square when the last data point was hit. Instead one only plots points, plotting the observed kth observed points (in order: formally the observed kth order statistic) against the k/(n + 1) quantile
of the theoretical distribution. This choice of "plotting position" (choice of quantile of the theoretical distribution) has occasioned less controversy than the choice for Q-Q plots.
The resulting goodness of fit of the 45° line gives a measure of the difference between a sample set and the theoretical distribution.
A P-P plot can be used as a graphical adjunct to a tests of the fit of probability distributions, with additional lines being included on the plot to indicate either specific acceptance regions or the range of expected departure from the 1:1 line. An improved version of the P-P plot, called the SP or S-P plot, is available, which makes use of a variance-stabilizing transformation
to create a plot on which the variations about the 1:1 line should be the same at all locations.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a P-P plot (probability-probability plot or percent-percent plot) is a probability plot
Probability plot
In statistics, a P-P plot is a probability plot for assessing how closely two data sets agree, which plots the two cumulative distribution functions against each other....
for assessing how closely two data set
Data set
A data set is a collection of data, usually presented in tabular form. Each column represents a particular variable. Each row corresponds to a given member of the data set in question. Its values for each of the variables, such as height and weight of an object or values of random numbers. Each...
s agree, which plots the two cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s against each other.
The Q-Q plot
Q-Q plot
In statistics, a Q-Q plot is a probability plot, which is a graphical method for comparing two probability distributions by plotting their quantiles against each other. First, the set of intervals for the quantiles are chosen...
is more widely used, but they are both referred to as "the" probability plot, and are potentially confused.
Definition
A P-P plot plots two cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s (cdfs) against each other:
given two probability distributions, with cdfs "F" and "G", it plots
 as z ranges from
as z ranges from 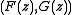 to
to  As a cdf has range [0,1], the domain of this parametric graph is
As a cdf has range [0,1], the domain of this parametric graph is 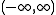 and the range is the unit square
and the range is the unit square 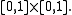
Thus for input z the output is the pair of numbers giving what percentage of f and what percentage of g fall at or below z.
The comparison line is the 45° line from (0,0) to (1,1) – the distributions are equal if and only if the plot falls on this line – any deviation indicates a difference between the distributions.
Example
As an example, if the two distributions do not overlap, say F is below G, then the P-P plot will move from left to right along the bottom of the square – as z moves through the support of F, the cdf of F goes from 0 to 1, while the cdf of G stays at 0 – and then moves up the right side of the square – the cdf of F is now 1, as all points of F lie below all points of G, and now the cdf of G moves from 0 to 1 as z moves through the support of G.Use
As this example illustrates, if two distributions are separated in space, the P-P plot will give very little data – it is only useful for comparing probability distributions that have nearby or equal location. Notably, it will pass through the point (1/2, 1/2) if and only if the two distributions have the same medianMedian
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
.
P-P plots are sometimes limited to comparisons between two samples, rather than comparison of a sample to a theoretical model distribution. However, they are of general use, particularly where observations are not all modelled with the same distribution.
However, it was found some use in comparing a sample distribution from a known theoretical distribution: given n samples, plotting the continuous theoretical cdf against the empirical cdf would yield a stair-step (a step as z hits a sample), and would hit the top of the square when the last data point was hit. Instead one only plots points, plotting the observed kth observed points (in order: formally the observed kth order statistic) against the k/(n + 1) quantile
Quantile
Quantiles are points taken at regular intervals from the cumulative distribution function of a random variable. Dividing ordered data into q essentially equal-sized data subsets is the motivation for q-quantiles; the quantiles are the data values marking the boundaries between consecutive subsets...
of the theoretical distribution. This choice of "plotting position" (choice of quantile of the theoretical distribution) has occasioned less controversy than the choice for Q-Q plots.
The resulting goodness of fit of the 45° line gives a measure of the difference between a sample set and the theoretical distribution.
A P-P plot can be used as a graphical adjunct to a tests of the fit of probability distributions, with additional lines being included on the plot to indicate either specific acceptance regions or the range of expected departure from the 1:1 line. An improved version of the P-P plot, called the SP or S-P plot, is available, which makes use of a variance-stabilizing transformation
Variance-stabilizing transformation
In applied statistics, a variance-stabilizing transformation is a data transformation that is specifically chosen either to simplify considerations in graphical exploratory data analysis or to allow the application of simple regression-based or analysis of variance techniques.The aim behind the...
to create a plot on which the variations about the 1:1 line should be the same at all locations.

