
Product form solution
Encyclopedia
In probability theory
, a product form solution is a particularly efficient form of solution for determining some metric of a system with distinct sub-components, where the metric for the collection of components can be written as a product of the metric across the different components. Using capital Pi notation a product form solution has algebraic form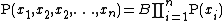
where B is some constant. Solutions of this form are of interest as they are computationally inexpensive to evaluate for large values of n. Such solutions in queueing networks are important for finding performance metrics in models of multiprogrammed and time-shared computer systems.
es. Trivially, models composed of two or more independent sub-components exhibit a product form solution by the definition of independence. Initially the term was used in queueing networks where the sub-components would be individual queues. For example, Jackson's theorem gives the joint equilibrium distribution of an open queueing network as the product of the equilibrium distributions of the individual queues. After numerous extensions, chiefly the BCMP network
it was thought local balance was a requirement for a product form solution. Gelenbe
's G-network model showed this to not be the case. Product form solutions are sometimes described as "stations are independent in equilibrium".
The search for processes with product form solutions continues as an active research area in queueing theory and other Markovian settings
such as Markov process algebras (e.g. PEPA
) and stochastic
timed petri nets. J.M. Harrison
and R.J. Williams note that "virtually all of the models that have been successfully analyzed in classical queueing network theory are models having a so-called product form stationary distribution"
For closed networks, Chow showed a result to hold for two service nodes, which was later generalised to a cycle of queues and to overtake–free paths in Gordon–Newell networks.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a product form solution is a particularly efficient form of solution for determining some metric of a system with distinct sub-components, where the metric for the collection of components can be written as a product of the metric across the different components. Using capital Pi notation a product form solution has algebraic form
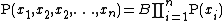
where B is some constant. Solutions of this form are of interest as they are computationally inexpensive to evaluate for large values of n. Such solutions in queueing networks are important for finding performance metrics in models of multiprogrammed and time-shared computer systems.
Equilibrium distributions
The first product form solutions were found for equilibrium distributions of Markov processMarkov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
es. Trivially, models composed of two or more independent sub-components exhibit a product form solution by the definition of independence. Initially the term was used in queueing networks where the sub-components would be individual queues. For example, Jackson's theorem gives the joint equilibrium distribution of an open queueing network as the product of the equilibrium distributions of the individual queues. After numerous extensions, chiefly the BCMP network
BCMP network
In queueing theory, a discipline within the mathematical theory of probability, a BCMP network is a class of queueing network for which a product form equilibrium distribution exists. It is named after the authors of the paper where the network was first described: Baskett, Chandy, Muntz and Palacios...
it was thought local balance was a requirement for a product form solution. Gelenbe
Erol Gelenbe
Sami Erol Gelenbe is a Turkish computer scientist, engineer and applied mathematician who currently holds the Dennis Gabor Professorship at Imperial College...
's G-network model showed this to not be the case. Product form solutions are sometimes described as "stations are independent in equilibrium".
The search for processes with product form solutions continues as an active research area in queueing theory and other Markovian settings
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
such as Markov process algebras (e.g. PEPA
PEPA
Performance Evaluation Process Algebra is a stochastic process algebra designed for modelling computer and communication systems introduced by Jane Hillston in the 1990s...
) and stochastic
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
timed petri nets. J.M. Harrison
J. Michael Harrison
J. Michael Harrison is an American scientist, known for his contributions to the theory of mathematical finance, in particularstochastic networks and financial engineering. He has authorednear 90 journal articles and written two books in his area....
and R.J. Williams note that "virtually all of the models that have been successfully analyzed in classical queueing network theory are models having a so-called product form stationary distribution"
Sojourn time distributions
The term product form has also been used to refer to the sojourn time distribution in a cyclic queueing system, where the time spent by jobs at M nodes is given as the product of time spent at each node. In 1957 Reich showed the result for two M/M/1 queues in tandem, later extending this to n M/M/1 queues in tandem and to overtake–free paths in Jackson networks. Walrand and Varaiya suggest that non-overtaking (where customers cannot overtake other customers by taking a different route through the network) may be a necessary condition for the result to hold. Mitrani offers exact solutions to some simple networks with overtaking, showing that none of these exhibit product form sojourn time distributions.For closed networks, Chow showed a result to hold for two service nodes, which was later generalised to a cycle of queues and to overtake–free paths in Gordon–Newell networks.

