
Projection method (fluid dynamics)
Encyclopedia
The projection method is an effective means of numerically
solving time-dependent incompressible fluid-flow
problems. It was originally introduced by Alexandre Chorin
in 1967 and independently by Roger Temam
as an efficient means of solving the incompressible Navier-Stokes equations. The key advantage of the projection method is that the computations of the velocity and the pressure fields are decoupled.
(sometimes called Helmholtz-Hodge decomposition) of any vector field into a solenoidal part and an irrotational part. Typically, the algorithm consists of two stages. In the first stage, an intermediate velocity that does not satisfy the incompressibility constraint is computed at each time step. In the second, the pressure is used to project the intermediate velocity onto a space of divergence-free velocity field to get the next update of velocity and pressure.
sometimes referred to as Helmholtz–Hodge Decomposition or simply as Hodge decomposition. It states that the vector field defined on a simply connected domain can be uniquely decomposed into a divergence-free (solenoidal) part
defined on a simply connected domain can be uniquely decomposed into a divergence-free (solenoidal) part 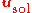 and an irrotational part
and an irrotational part  . Thus,
. Thus,

since for some scalar function,
for some scalar function,  . Taking the
. Taking the
divergence of equation yields

This is a Poisson equation for the scalar function . If the vector field
. If the vector field  is known, the above equation can be solved for the scalar function
is known, the above equation can be solved for the scalar function  and the divergence part of
and the divergence part of  can be extracted using the relation
can be extracted using the relation
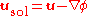
This is the essence of solenoidal projection method for solving incompressible
Navier–Stokes equations.
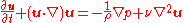
In Chorin's original version of the projection method
, the intermediate velocity,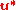 , is explicitly computed using the momentum equation ignoring the pressure gradient term:
, is explicitly computed using the momentum equation ignoring the pressure gradient term:
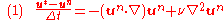
where is the velocity at
is the velocity at  th time level. In the next (projection) step, we have
th time level. In the next (projection) step, we have
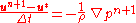
Re-writing the above equation for the velocity at level, we have
level, we have
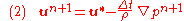
Computing the right-hand side of the above equation requires a knowledge of the pressure,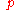 , at
, at  level. This is obtained by taking the divergence
level. This is obtained by taking the divergence
and requiring that , which is the divergence-free(continuity) condition, thereby deriving the following Poisson equation for
, which is the divergence-free(continuity) condition, thereby deriving the following Poisson equation for 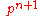 ,
,
It is instructive to note that, the equation written in the following way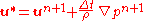
is the standard Hodge decomposition if boundary condition for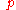 on the domain boundary,
on the domain boundary,  is
is  .
.
For the explicit method, the boundary condition for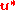 in equation (1) is natural. If
in equation (1) is natural. If  on
on  , is prescribed, then the space of divergence-free vector field will be orthogonal to the space of irrotational vector fields, and from equation (2) one has
, is prescribed, then the space of divergence-free vector field will be orthogonal to the space of irrotational vector fields, and from equation (2) one has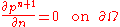
The explicit treatment of the boundary condition may be circumvented by using a staggered grid and requiring that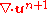 vanish at the pressure nodes that are adjacent to the boundaries.
vanish at the pressure nodes that are adjacent to the boundaries.
A distinguishing feature of Chorin's projection method is that the velocity field is forced to satisfy a discrete continuity constraint at the end of each time step.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
solving time-dependent incompressible fluid-flow
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
problems. It was originally introduced by Alexandre Chorin
Alexandre Chorin
Alexandre J. Chorin is a professor of mathematics at the University of California, Berkeley who works in applied mathematics. He is known for his contributions to the field of Computational fluid dynamics....
in 1967 and independently by Roger Temam
Roger Temam
Roger Meyer Temam is a College Professor of mathematics at The Indiana University, Bloomington. According to Mathematics Genealogy Project, Temam has supervised 106 PhD thesis; this is the highest number PhD thesis supervised by an individual in the field of mathematics. He has a total of 314...
as an efficient means of solving the incompressible Navier-Stokes equations. The key advantage of the projection method is that the computations of the velocity and the pressure fields are decoupled.
The algorithm
The algorithm of projection method is based on the Helmholtz decompositionHelmholtz decomposition
In physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational vector field and a...
(sometimes called Helmholtz-Hodge decomposition) of any vector field into a solenoidal part and an irrotational part. Typically, the algorithm consists of two stages. In the first stage, an intermediate velocity that does not satisfy the incompressibility constraint is computed at each time step. In the second, the pressure is used to project the intermediate velocity onto a space of divergence-free velocity field to get the next update of velocity and pressure.
Helmholtz–Hodge decomposition
The theoretical background of projection type method is the decomposition theorem of LadyzhenskayaOlga Aleksandrovna Ladyzhenskaya
Olga Aleksandrovna Ladyzhenskaya was a Soviet and Russian mathematician. She was known for her work on partial differential equations and fluid dynamics...
sometimes referred to as Helmholtz–Hodge Decomposition or simply as Hodge decomposition. It states that the vector field
 defined on a simply connected domain can be uniquely decomposed into a divergence-free (solenoidal) part
defined on a simply connected domain can be uniquely decomposed into a divergence-free (solenoidal) part 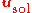 and an irrotational part
and an irrotational part  . Thus,
. Thus,
since
 for some scalar function,
for some scalar function,  . Taking the
. Taking thedivergence of equation yields

This is a Poisson equation for the scalar function
 . If the vector field
. If the vector field  is known, the above equation can be solved for the scalar function
is known, the above equation can be solved for the scalar function  and the divergence part of
and the divergence part of  can be extracted using the relation
can be extracted using the relation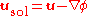
This is the essence of solenoidal projection method for solving incompressible
Navier–Stokes equations.
Chorin's projection method
The incompressible Navier-Stokes equation (differential form of momentum equation) may be written as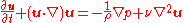
In Chorin's original version of the projection method
, the intermediate velocity,
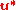 , is explicitly computed using the momentum equation ignoring the pressure gradient term:
, is explicitly computed using the momentum equation ignoring the pressure gradient term: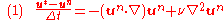
where
 is the velocity at
is the velocity at  th time level. In the next (projection) step, we have
th time level. In the next (projection) step, we have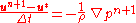
Re-writing the above equation for the velocity at
 level, we have
level, we have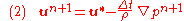
Computing the right-hand side of the above equation requires a knowledge of the pressure,
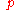 , at
, at  level. This is obtained by taking the divergence
level. This is obtained by taking the divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
and requiring that
 , which is the divergence-free(continuity) condition, thereby deriving the following Poisson equation for
, which is the divergence-free(continuity) condition, thereby deriving the following Poisson equation for 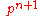 ,
,
It is instructive to note that, the equation written in the following way
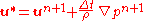
is the standard Hodge decomposition if boundary condition for
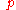 on the domain boundary,
on the domain boundary,  is
is  .
.For the explicit method, the boundary condition for
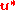 in equation (1) is natural. If
in equation (1) is natural. If  on
on  , is prescribed, then the space of divergence-free vector field will be orthogonal to the space of irrotational vector fields, and from equation (2) one has
, is prescribed, then the space of divergence-free vector field will be orthogonal to the space of irrotational vector fields, and from equation (2) one has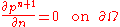
The explicit treatment of the boundary condition may be circumvented by using a staggered grid and requiring that
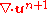 vanish at the pressure nodes that are adjacent to the boundaries.
vanish at the pressure nodes that are adjacent to the boundaries.A distinguishing feature of Chorin's projection method is that the velocity field is forced to satisfy a discrete continuity constraint at the end of each time step.
General method
Typically the projection method operates as a two-stage fractional step scheme, a method which uses multiple calculation steps for each numerical time-step. In many projection algorithms, the steps are split as follows:- First the system is progressed in time to a mid-time-step position, solving the above transport equations for mass and momentum using a suitable advection method. This is denoted the predictor step.
- At this point an initial projection may be implemented such that the mid-time-step velocity field is enforced as divergence free.
- The corrector part of the algorithm is then progressed. These use the time-centred estimates of the velocity, density, etc. to form final time-step state.
- A final projection is then applied to enforce the divergence restraint on the velocity field. The system has now been fully updated to the new time.

