Proof by contrapositive
Encyclopedia
In logic
, the contrapositive of a conditional
statement of the form "if A then B" is formed by negating both terms and reversing the direction of inference. Thus, the contrapositive of the statement "if A, then B" is "if not B, then not A." A statement and its contrapositive are logically equivalent: if the statement is true, then its contrapositive is true, and vice versa.
In logic, proof by contrapositive is a form of proof
that establishes the truth or validity
of a proposition
by demonstrating the truth or validity of the converse of its negated parts.
In other words, to prove by contraposition that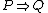
, prove that 
.
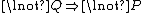It has similarities to the Proof by contradiction, where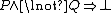
is proven in order to show 
.
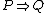See main article on contraposition: Contraposition (traditional logic).
A direct proof
is difficult, so a proof by contrapositive is preferable.
Suppose x is not even, that is, x is odd. Then x = 2k + 1, for some whole number k.
So x2 = (2k +1)2 = 4k2 + 4k + 1 = 2(2k2 + 2k) + 1 which is odd.
Thus we have proved: if x is not even, then the square of x is not even.
So by contrapositive: if the square of x is even, x is even.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, the contrapositive of a conditional
Indicative conditional
In natural languages, an indicative conditional is the logical operation given by statements of the form "If A then B". Unlike the material conditional, an indicative conditional does not have a stipulated definition...
statement of the form "if A then B" is formed by negating both terms and reversing the direction of inference. Thus, the contrapositive of the statement "if A, then B" is "if not B, then not A." A statement and its contrapositive are logically equivalent: if the statement is true, then its contrapositive is true, and vice versa.
In logic, proof by contrapositive is a form of proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
that establishes the truth or validity
Validity
In logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
of a proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
by demonstrating the truth or validity of the converse of its negated parts.
In other words, to prove by contraposition that
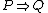, prove that 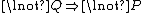.It has similarities to the Proof by contradiction, where
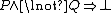is proven in order to show 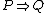.See main article on contraposition: Contraposition (traditional logic).
Example
To prove: For all whole numbers x, if x2 is even then x is even.A direct proof
Direct proof
In mathematics and logic, a direct proof is a way of showing the truth or falsehood of a given statement by a straightforward combination of established facts, usually existing lemmas and theorems, without making any further assumptions...
is difficult, so a proof by contrapositive is preferable.
Suppose x is not even, that is, x is odd. Then x = 2k + 1, for some whole number k.
So x2 = (2k +1)2 = 4k2 + 4k + 1 = 2(2k2 + 2k) + 1 which is odd.
Thus we have proved: if x is not even, then the square of x is not even.
So by contrapositive: if the square of x is even, x is even.
See also
- Modus tollensModus tollensIn classical logic, modus tollens has the following argument form:- Formal notation :...
- Proof by contradiction
- Reductio ad absurdumReductio ad absurdumIn logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
- Mathematical proofMathematical proofIn mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...