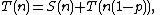Prune and search is a method of solving optimization

Optimization (mathematics)

In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....

 problems suggested by Nimrod Megiddo

Nimrod Megiddo

Nimrod Megiddo is a mathematician and computer scientist. He is research scientist at the IBM Almaden Research Center.His interests include optimization, algorithm design and analysis, game theory, and machine learning....

 in 1983.

The basic idea of the method is a recursive procedure in which at each step the input size is reduced ("pruned") by a constant factor 0 < p < 1. Let n be the input size, T(n) be the time complexity

Time complexity

In computer science, the time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the size of the input to the problem. The time complexity of an algorithm is commonly expressed using big O notation, which suppresses multiplicative constants and...

 of the whole prune-and-search algorithm, S(n) is the time complexity of the pruning step, then T(n) obeys the following recurrence relation

Recurrence relation

In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....

:

which has the solution T(n) = O(S(n)).

In particular, Megiddo himself used this approach in his linear time algorithm for the linear programming

Linear programming

Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...

 problem when the dimension is fixed and for the minimal enclosing circle problem for a set of points in the plane.