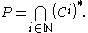Pseudo-arc
Encyclopedia
In general topology
, the pseudo-arc is the simplest nondegenerate hereditarily indecomposable
continuum
. Pseudo-arc is an arc-like homogeneous continuum. R.H. Bing proved that, in a certain well-defined sense, most continua in Rn, n ≥ 2, are homeomorphic to the pseudo-arc.
asked whether a nondegenerate homogeneous continuum in the Euclidean plane R2 must be a Jordan curve. In 1921, Stefan Mazurkiewicz
asked whether a nondegenerate continuum in R2 that is homeomorphic to each of its nondegenerate subcontinua must be an arc. In 1922, Knaster described the first example of a homogeneous hereditarily indecomposable continuum K. In 1948, R.H. Bing constructed a continuum B giving a negative answer to the Knaster–Kuratowski question and Edwin Moise
constructed a continuum M giving a negative answer to the Mazurkiewicz question. Due to its resemblance to the fundamental property of the arc, namely, being homeomorphic to all its nondegenerate subcontinua, Moise called his example M a pseudo-arc and showed that it was hereditarily indecomposable. Bing's construction of B is a modification of Moise's construction of M, which he had first heard described in a lecture. In 1951, Bing proved that all hereditarily indecomposable arc-like continua are homeomorphic — this implies that Knaster's K, Moise's M, and Bing's B are all homeomorphic. Bing also proved that the pseudo-arc is typical among the continua in a Euclidean space of dimension at least 2 or an infinite-dimensional separable Hilbert space
.
While being the simplest of the type of spaces listed above, the pseudo-arc is actually very complex. The concept of a chain being crooked (defined below) is what endows the pseudo-arc with its complexity. Informally, it requires a chain to follow a certain recursive
zig-zag pattern in another chain. To 'move' from the mth link of the larger chain to the nth, the smaller chain must first move in a crooked manner from the mth link to the (n-1)th link, then in a crooked manner to the (m+1)th link, and then finally to the nth link.
More formally:
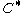 denote the union of all of the elements of C. That is, let
denote the union of all of the elements of C. That is, let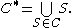
The pseudo-arc is defined as follows:
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
, the pseudo-arc is the simplest nondegenerate hereditarily indecomposable
Indecomposable continuum
In point-set topology, an indecomposable continuum is a continuum that is not the union of any two of its proper subcontinua. The pseudo-arc is an example of a hereditarily indecomposable continuum. L. E. J...
continuum
Continuum (topology)
In the mathematical field of point-set topology, a continuum is a nonempty compact connected metric space, or less frequently, a compact connected Hausdorff topological space...
. Pseudo-arc is an arc-like homogeneous continuum. R.H. Bing proved that, in a certain well-defined sense, most continua in Rn, n ≥ 2, are homeomorphic to the pseudo-arc.
History
In 1920, Bronisław Knaster and Kazimierz KuratowskiKazimierz Kuratowski
Kazimierz Kuratowski was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics.-Biography and studies:...
asked whether a nondegenerate homogeneous continuum in the Euclidean plane R2 must be a Jordan curve. In 1921, Stefan Mazurkiewicz
Stefan Mazurkiewicz
Stefan Mazurkiewicz was a Polish mathematician who worked in mathematical analysis, topology, and probability. He was a student of Wacław Sierpiński and a member of the Polish Academy of Learning...
asked whether a nondegenerate continuum in R2 that is homeomorphic to each of its nondegenerate subcontinua must be an arc. In 1922, Knaster described the first example of a homogeneous hereditarily indecomposable continuum K. In 1948, R.H. Bing constructed a continuum B giving a negative answer to the Knaster–Kuratowski question and Edwin Moise
Edwin E. Moise
Edwin Evariste Moise was an American mathematician and mathematics education reformer. After his retirement from mathematics he became a literary critic of 19th century English poetry and had several notes published in that field.-Early life and education:...
constructed a continuum M giving a negative answer to the Mazurkiewicz question. Due to its resemblance to the fundamental property of the arc, namely, being homeomorphic to all its nondegenerate subcontinua, Moise called his example M a pseudo-arc and showed that it was hereditarily indecomposable. Bing's construction of B is a modification of Moise's construction of M, which he had first heard described in a lecture. In 1951, Bing proved that all hereditarily indecomposable arc-like continua are homeomorphic — this implies that Knaster's K, Moise's M, and Bing's B are all homeomorphic. Bing also proved that the pseudo-arc is typical among the continua in a Euclidean space of dimension at least 2 or an infinite-dimensional separable Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
.
Chains
At the heart of the definition of the pseudo-arc is the concept of a chain, which is defined as follows:- A chain is a finite collection of open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s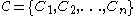 in a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
in a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
such that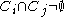 if and only if
if and only if 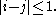 The elements of a chain are called its links, and a chain is called an ε-chain if each of its links has diameterDiameterIn geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
The elements of a chain are called its links, and a chain is called an ε-chain if each of its links has diameterDiameterIn geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
less than ε.
While being the simplest of the type of spaces listed above, the pseudo-arc is actually very complex. The concept of a chain being crooked (defined below) is what endows the pseudo-arc with its complexity. Informally, it requires a chain to follow a certain recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
zig-zag pattern in another chain. To 'move' from the mth link of the larger chain to the nth, the smaller chain must first move in a crooked manner from the mth link to the (n-1)th link, then in a crooked manner to the (m+1)th link, and then finally to the nth link.
More formally:
- Let
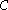 and
and 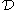 be chains such that
be chains such that
-
- each link of
 is a subset of a link of
is a subset of a link of 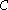 , and
, and - for any indices i, j, m, and n with
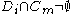 ,
,  , and
, and 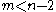 , there exist indices
, there exist indices 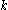 and
and 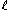 with
with 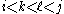 (or
(or  ) and
) and 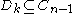 and
and 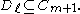
- each link of
- Then
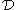 is crooked in
is crooked in 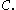
Pseudo-arc
For any collect C of sets, let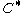 denote the union of all of the elements of C. That is, let
denote the union of all of the elements of C. That is, let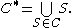
The pseudo-arc is defined as follows:
- Let p and q be distinct points in the plane and
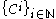 be a sequence of chains in the plane such that for each i,
be a sequence of chains in the plane such that for each i,
-
- the first link of
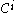 contains p and the last link contains q,
contains p and the last link contains q, - the chain
 is a
is a  -chain,
-chain, - the closure of each link of
 is a subset of some link of
is a subset of some link of  , and
, and - the chain
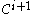 is crooked in
is crooked in 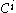 .
.
- the first link of
- Let
- Then P is a pseudo-arc.