Pseudocircle
Encyclopedia
The pseudocircle is the finite topological space
X consisting of four distinct points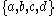
with the following non-Hausdorff
topology: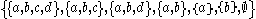
X is highly pathological
from the viewpoint of general topology
as it fails to satisfy any separation axiom
besides T0
. However from the viewpoint of algebraic topology
X has the remarkable property that it is indistinguishable from the unit circle
.
More precisely the map
given by
is a weak homotopy equivalence
, that is f induces an isomorphism on all homotopy groups. It follows (proposition 4.21 in Hatcher) that f also induces an isomorphism on singular homology and cohomology
and more generally an isomorphism on all extraordinary homology and cohomology theories
(e.g. K-theory
).
This can be proved using the following observation. Like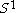
, X is the union of two contractible open sets 
and 
whose intersection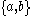 
is also the union of two contractible open sets 
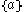and 
.
More generally McCord has shown that for any finite simplicial complex
K, there is a finite topological space
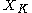which has the same weak homotopy type as the geometric realization
|K| of K. More precisely there is a functor
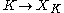from the category of finite simplicial complexes and simplicial maps and a natural
weak homotopy equivalence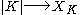
.
Finite topological space
In mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
X consisting of four distinct points
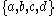with the following non-HausdorffHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topology:
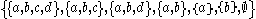
X is highly pathological
Pathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
from the viewpoint of general topology
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
as it fails to satisfy any separation axiom
Separation axiom
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
besides T0
Kolmogorov space
In topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
. However from the viewpoint of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
X has the remarkable property that it is indistinguishable from the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
.More precisely the map
given byis a weak homotopy equivalence
Whitehead theorem
In homotopy theory , the Whitehead theorem states that if a continuous mapping f between topological spaces X and Y induces isomorphisms on all homotopy groups, then f is a homotopy equivalence provided X and Y are connected and have the homotopy-type of CW complexes. This result was proved by J....
, that is f induces an isomorphism on all homotopy groups. It follows (proposition 4.21 in Hatcher) that f also induces an isomorphism on singular homology and cohomology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
and more generally an isomorphism on all extraordinary homology and cohomology theories
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
(e.g. K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
).
This can be proved using the following observation. Like
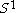, X is the union of two contractible open sets and whose intersection 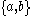is also the union of two contractible open sets 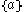and .More generally McCord has shown that for any finite simplicial complex
Abstract simplicial complex
In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...
K, there is a finite topological space
Finite topological space
In mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
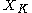which has the same weak homotopy type as the geometric realizationAbstract simplicial complex
In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...
|K| of K. More precisely there is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
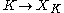from the category of finite simplicial complexes and simplicial maps and a naturalNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
weak homotopy equivalence
.
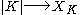