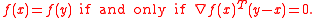Pseudolinear function
Encyclopedia
In mathematics, a pseudoconvex function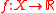 
on an open convex set 
is a function that is differentiable in 
such that for every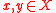 
,
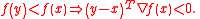
It is pseudoconcave if this is true of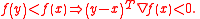
.
A pseudolinear function is one that is both pseudoconvex and pseudoconcave.
It can be shown (see Cambini and Martein) that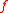
is pseudolinear if and only if for every 
,
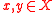In mathematical optimization, linear–fractional program
s have pseudolinear objective functions and linear–inequality constraints
: These properties allow linear-fractional problems to be solved by a variant of the simplex algorithm
(of George B. Dantzig).
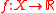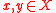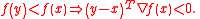
on an open convex set is a function that is differentiable in such that for every ,It is pseudoconcave if this is true of
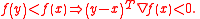.A pseudolinear function is one that is both pseudoconvex and pseudoconcave.
It can be shown (see Cambini and Martein) that
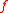is pseudolinear if and only if for every ,
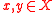In mathematical optimization, linear–fractional program
Linear-fractional programming
In mathematical optimization, linear-fractional programming is a generalization of linear programming . Whereas the objective function in linear programs are linear functions, the objective function in a linear-fractional program is a ratio of two linear functions...
s have pseudolinear objective functions and linear–inequality constraints
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
: These properties allow linear-fractional problems to be solved by a variant of the simplex algorithm
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
(of George B. Dantzig).