
Pseudomathematics
Encyclopedia
Pseudomathematics is a form of mathematics
-like activity that does not work within the framework, definitions, rules, or rigor of formal
mathematical models. While any given pseudomathematical approach may work within some of these boundaries, for instance, by accepting or invoking most known mathematical definitions that apply, pseudomathematics inevitably disregards or explicitly discards a well-established or proven mechanism, falling back upon any number of demonstrably non-mathematical principles.
----
----
While the above "proof" suffers from various flaws (such as the flawed invocation of mathematical induction
and there is no agreement that 1 is a prime), all that is required to topple it is to show a counterexample
, such as the positive integer 33. This number is not prime, and if it is shown by way of arriving at a contradiction that numbers evenly divisible by any number (other than 1 or themselves) are not prime (by definition) and this thus contradicts the definition of primes, the counterargument might make an appeal such as "then the definition of primes is flawed since the above proof shows that numbers such as 33 (which is not divisible by 2) are prime."
In mathematics, a statement presenting itself as a mathematical truth is provably incorrect (that is, not a mathematical truth statement) if even one counterexample
showing it to be false can be found. Indeed, a statement cannot rightly be called a "theorem
" if a counterexample disproving it exists. While it is possible to call something a conjecture
until a full formal proof is provided, until and unless that proof is provided, it does not become a theorem. Conjectures, too, may be shown to be false if a counterexample exists.
An appeal that a mathematical definition is in itself wrong (i.e., that primes were somehow poorly defined in the first place) is an appeal to an argument that attacks a well-established and well-understood definition: Primes are prime by definition, and such classes of numbers may or may not have properties that make them interesting. Pseudomathematics, however, sometimes appeals to change definitions to suit its claims. At this point, pseudomathematical arguments exit the world of mathematics altogether, and even the appearance of following long-established mathematical models falls apart.
Any statement purporting to be a theorem must hold within the framework of the pre-existing definitions about which it purports to assert a truth. While new definitions may be introduced into a framework to substantiate a theorem, these new definitions must themselves hold within the framework addressed, without introducing any contradiction within that framework. Asserting that 33 is somehow prime because a flawed proof arrives at this eventuality, and then asserting that the definition of primes itself is flawed is pseudomathematical reasoning.
Examples of impossible problems include the following constructions in Euclidean geometry
using only compass and straightedge
:
For more than 2,000 years many people have tried and failed to find such constructions; the reasons were discovered in the 19th century, when it was proved that they are all impossible. This category also extends to attempts to disprove accepted (and proven) mathematical theorems such as Cantor's diagonal argument
and Gödel's incompleteness theorem.
, where various efforts are made to continually attempt to invent perpetual motion
devices, disprove Einstein
using Newtonian mechanics, and other feats that are currently accepted as impossible.
Excessive pursuit of pseudomathematics can result in the practitioner being labelled a crank
. The topic of mathematical "crankiness" has been extensively studied by Indiana mathematician Underwood Dudley
, who has written several popular works about mathematical cranks and their ideas.
Not all mathematical research undertaken by amateur mathematicians is pseudomathematics. Amateur mathematicians have produced genuinely solid new mathematical results. Indeed, there is no distinction between an amateur mathematically correct result and a professional mathematically correct result; results either are, or are not correct, and pseudomathematical results, by relying on non-mathematical principles, are not about professionalism but about incorrectness arrived at by improper methodology.
or the Riemann hypothesis
using elementary mathematical techniques (second category). Fermat's theorem now has a lengthy and extremely technical orthodox proof drawing on many different areas of advanced mathematics. Even so, numerous attempts have been made to either overturn the orthodox proof or to provide a more "elementary" proof closer to the implied "simple" proof to which Fermat is conjectured to have alluded. (Such attempts are not pseudomathematical unless accepted mathematical methods are disregarded; perhaps there really is an uncorrectable error in the published proof, and it has not been conclusively demonstrated that Fermat was mistaken in his supposed "proof" or that some other "simpler" proof cannot be found.)
Other related activities include attempts to create lossless data compression
algorithms which will compress all possible inputs or to disprove the four-color theorem; both of these belong to the first category of problems proven to be impossible (assuming that there is no significant error in the accepted proof of the latter). In the former case, there is a trivial proof of impossibility—such an algorithm would need to map a finite large set of input onto a smaller set of output on a one-to-one basis.
Other common subjects of pseudomathematicians include the meaning of infinity
, the nature of complex number
s, and the indeterminate
expression 0/0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
-like activity that does not work within the framework, definitions, rules, or rigor of formal
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
mathematical models. While any given pseudomathematical approach may work within some of these boundaries, for instance, by accepting or invoking most known mathematical definitions that apply, pseudomathematics inevitably disregards or explicitly discards a well-established or proven mechanism, falling back upon any number of demonstrably non-mathematical principles.
An illustrative contrived example
Consider the following flawed attempt at a theorem:----
- Theorem: All positive odd numbers are primePrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
.
- Proof: By mathematical inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
.
- Let
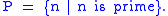
- Let n = 1. Then n ∈ P.
- Since n + 1 ∈ P and (n + 1) + 1 ∈ P, and skipping those divisible by 2, all numbers are prime (except those that are divisible by 2), due to induction.
- Q.E.D.Q.E.D.Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
----
While the above "proof" suffers from various flaws (such as the flawed invocation of mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
and there is no agreement that 1 is a prime), all that is required to topple it is to show a counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
, such as the positive integer 33. This number is not prime, and if it is shown by way of arriving at a contradiction that numbers evenly divisible by any number (other than 1 or themselves) are not prime (by definition) and this thus contradicts the definition of primes, the counterargument might make an appeal such as "then the definition of primes is flawed since the above proof shows that numbers such as 33 (which is not divisible by 2) are prime."
In mathematics, a statement presenting itself as a mathematical truth is provably incorrect (that is, not a mathematical truth statement) if even one counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
showing it to be false can be found. Indeed, a statement cannot rightly be called a "theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
" if a counterexample disproving it exists. While it is possible to call something a conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
until a full formal proof is provided, until and unless that proof is provided, it does not become a theorem. Conjectures, too, may be shown to be false if a counterexample exists.
An appeal that a mathematical definition is in itself wrong (i.e., that primes were somehow poorly defined in the first place) is an appeal to an argument that attacks a well-established and well-understood definition: Primes are prime by definition, and such classes of numbers may or may not have properties that make them interesting. Pseudomathematics, however, sometimes appeals to change definitions to suit its claims. At this point, pseudomathematical arguments exit the world of mathematics altogether, and even the appearance of following long-established mathematical models falls apart.
Any statement purporting to be a theorem must hold within the framework of the pre-existing definitions about which it purports to assert a truth. While new definitions may be introduced into a framework to substantiate a theorem, these new definitions must themselves hold within the framework addressed, without introducing any contradiction within that framework. Asserting that 33 is somehow prime because a flawed proof arrives at this eventuality, and then asserting that the definition of primes itself is flawed is pseudomathematical reasoning.
Some taxonomy of pseudomathematics
The following categories are rough characterisations of some particularly common pseudomathematical activities:- Attempting to solve classical problemProblemA problem is an obstacle, impediment, difficulty or challenge, or any situation that invites resolution; the resolution of which is recognized as a solution or contribution toward a known purpose or goal...
s in terms that have been proven mathematically impossibleLogical possibilityA logically possible proposition is one that can be asserted without implying a logical contradiction. This is to say that a proposition is logically possible if there is some coherent way for the world to be, under which the proposition would be true...
; - Misapprehending standard mathematical methods, and insisting that use or knowledge of higher mathematics is somehow cheating or misleading.
Attempts on classic unsolvable problems
Investigations in the first category are doomed to failure. At the very least a solution would indicate a contradiction within mathematics itself, a radical difficulty which would invalidate everyone's efforts to prove anything as trite.Examples of impossible problems include the following constructions in Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
using only compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
:
- Squaring the circleSquaring the circleSquaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...
: Given any circle drawing a square having the same area. - Doubling the cubeDoubling the cubeDoubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction...
: Given any cube drawing a cube with twice its volume. - Trisecting the angle: Given any angle dividing it into three smaller angles all of the same size.
For more than 2,000 years many people have tried and failed to find such constructions; the reasons were discovered in the 19th century, when it was proved that they are all impossible. This category also extends to attempts to disprove accepted (and proven) mathematical theorems such as Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
and Gödel's incompleteness theorem.
Practitioners
Pseudomathematics has equivalents in other scientific fields, particularly physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, where various efforts are made to continually attempt to invent perpetual motion
Perpetual motion
Perpetual motion describes hypothetical machines that operate or produce useful work indefinitely and, more generally, hypothetical machines that produce more work or energy than they consume, whether they might operate indefinitely or not....
devices, disprove Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
using Newtonian mechanics, and other feats that are currently accepted as impossible.
Excessive pursuit of pseudomathematics can result in the practitioner being labelled a crank
Crank (person)
"Crank" is a pejorative term used for a person who unshakably holds a belief that most of his or her contemporaries consider to be false. A "cranky" belief is so wildly at variance with commonly accepted belief as to be ludicrous...
. The topic of mathematical "crankiness" has been extensively studied by Indiana mathematician Underwood Dudley
Underwood Dudley
Underwood Dudley is a mathematician, formerly of DePauw University, who has written a number of research works and textbooks but is best known for his popular writing. Most notable are several books describing crank mathematics by people who think they have squared the circle or done other...
, who has written several popular works about mathematical cranks and their ideas.
Not all mathematical research undertaken by amateur mathematicians is pseudomathematics. Amateur mathematicians have produced genuinely solid new mathematical results. Indeed, there is no distinction between an amateur mathematically correct result and a professional mathematically correct result; results either are, or are not correct, and pseudomathematical results, by relying on non-mathematical principles, are not about professionalism but about incorrectness arrived at by improper methodology.
Current trends in pseudomathematics
In recent years, pseudomathematicians have devoted their energies to disproving Gödel's second incompleteness theorem (efforts that fall in the first category mentioned above) and to proving Fermat's Last TheoremFermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
or the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
using elementary mathematical techniques (second category). Fermat's theorem now has a lengthy and extremely technical orthodox proof drawing on many different areas of advanced mathematics. Even so, numerous attempts have been made to either overturn the orthodox proof or to provide a more "elementary" proof closer to the implied "simple" proof to which Fermat is conjectured to have alluded. (Such attempts are not pseudomathematical unless accepted mathematical methods are disregarded; perhaps there really is an uncorrectable error in the published proof, and it has not been conclusively demonstrated that Fermat was mistaken in his supposed "proof" or that some other "simpler" proof cannot be found.)
Other related activities include attempts to create lossless data compression
Lossless data compression
Lossless data compression is a class of data compression algorithms that allows the exact original data to be reconstructed from the compressed data. The term lossless is in contrast to lossy data compression, which only allows an approximation of the original data to be reconstructed, in exchange...
algorithms which will compress all possible inputs or to disprove the four-color theorem; both of these belong to the first category of problems proven to be impossible (assuming that there is no significant error in the accepted proof of the latter). In the former case, there is a trivial proof of impossibility—such an algorithm would need to map a finite large set of input onto a smaller set of output on a one-to-one basis.
Other common subjects of pseudomathematicians include the meaning of infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
, the nature of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, and the indeterminate
Indeterminate form
In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...
expression 0/0.
See also
- 0.999...0.999...In mathematics, the repeating decimal 0.999... denotes a real number that can be shown to be the number one. In other words, the symbols 0.999... and 1 represent the same number...
often claimed to be distinct from 1 - Eccentricity (behavior)Eccentricity (behavior)In popular usage, eccentricity refers to unusual or odd behavior on the part of an individual. This behavior would typically be perceived as unusual or unnecessary, without being demonstrably maladaptive...
- Invalid proofInvalid proofIn mathematics, certain kinds of mistakes in proof, calculation, or derivation are often exhibited, and sometimes collected, as illustrations of the concept of mathematical fallacy...
Further reading
- Underwood Dudley (1992), Mathematical Cranks, Mathematical Association of America. ISBN 0-88385-507-0.
- Underwood Dudley (1996), The Trisectors, Mathematical Association of America. ISBN 0-88385-514-3.
- Underwood Dudley (1997), Numerology: Or, What Pythagoras Wrought, Mathematical Association of America. ISBN 0-88385-524-0.
- Clifford Pickover (1999), Strange Brains and Genius, Quill. ISBN 0-688-16894-9.

