In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, Pugh's closing lemma is a result that links periodic orbit

Orbit (dynamics)

In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...

 solutions of differential equations

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

 to chaotic behaviour

Chaos theory

Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...

. It can be formally stated as follows:

Let 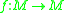be a diffeomorphism

Diffeomorphism

In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...

 of a compact

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

  smooth manifold

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

 . Given a nonwandering point

Wandering set

In those branches of mathematics called dynamical systems and ergodic theory, the concept of a wandering set formalizes a certain idea of movement and mixing in such systems. When a dynamical system has a wandering set of non-zero measure, then the system is a dissipative system...

  of 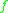, there exists a diffeomorphism 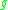arbitrarily close to in the 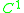topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

 of such that is a periodic point

Periodic point

In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time.- Iterated functions :...

 of .

Interpretation

Pugh's closing lemma means, for example, that any chaotic set in a bounded continuous dynamical system

Dynamical system

A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...

 corresponds to a periodic orbit in a different but closely related dynamical system. As such, an open set of conditions on a bounded continuous dynamical system that rules out periodic behaviour also implies that the system cannot behave chaotically; this is the basis of some autonomous convergence theorem

Autonomous convergence theorem

In mathematics, an autonomous convergence theorem is one of a family of related theorems which specify conditions guaranteeing global asymptotic stability of a continuous autonomous dynamical system.-History:...

s.