Purification of quantum state
Encyclopedia
In quantum mechanics
, especially quantum information
, purification refers to the fact that every mixed state acting on finite dimensional Hilbert spaces can be viewed as the reduced state
of some pure state.
In purely linear algebraic terms, it can be viewed as a statement about positive-semidefinite matrices.
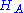of finite dimension n. Then there exist a Hilbert space 
and a pure state 
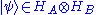such that the partial trace of 
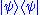with respect to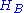 
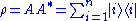. Let 
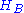be another copy of the n-dimensional Hilbert space with any orthonormal basis 
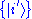. Define 
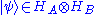by
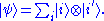
Direct calculation gives
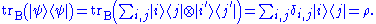
This proves the claim.
and purification of a mixed state, we can recover the Stinespring dilation theorem
for the finite dimensional case.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, especially quantum information
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
, purification refers to the fact that every mixed state acting on finite dimensional Hilbert spaces can be viewed as the reduced state
Partial trace
In linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function...
of some pure state.
In purely linear algebraic terms, it can be viewed as a statement about positive-semidefinite matrices.
Statement
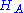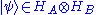Let ρ be a density matrix acting on a Hilbert space of finite dimension n. Then there exist a Hilbert space and a pure state such that the partial trace of 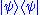with respect to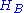 Proof
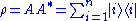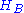A density matrix is by definition positive semidefinite. So ρ has square root factorization. Let be another copy of the n-dimensional Hilbert space with any orthonormal basis 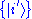. Define 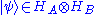by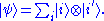Direct calculation gives
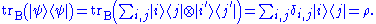
This proves the claim.
Note
- The vectorial pure state
is in the form specified by the Schmidt decompositionSchmidt decompositionIn linear algebra, the Schmidt decomposition refers to a particular way of expressing a vector in the tensor product of two inner product spaces. It has applications in quantum information theory and plasticity....
.
- Since square root decompositions of a positive semidefinite matrix are not unique, neither are purifications.
- In linear algebraic terms, a square matrix is positive semidefinite if and only if it can be purified in the above sense. The if part of the implication follows immediately from the fact that the partial tracePartial traceIn linear algebra and functional analysis, the partial trace is a generalization of the trace. Whereas the trace is a scalar valued function on operators, the partial trace is an operator-valued function...
is a positive mapChoi's theorem on completely positive mapsIn mathematics, Choi's theorem on completely positive maps is a result that classifies completely positive maps between finite-dimensional C*-algebras...
.
An application: Stinespring's theorem
By combining Choi's theorem on completely positive mapsChoi's theorem on completely positive maps
In mathematics, Choi's theorem on completely positive maps is a result that classifies completely positive maps between finite-dimensional C*-algebras...
and purification of a mixed state, we can recover the Stinespring dilation theorem
Stinespring factorization theorem
In mathematics, Stinespring's dilation theorem, also called Stinespring's factorization theorem, named after W. Forrest Stinespring, is a result from operator theory that represents any completely positive map on a C*-algebra as a composition of two completely positive maps each of which has a...
for the finite dimensional case.