Quantum no-deleting theorem
Encyclopedia
Quantum states are fragile in one sense and also robust in another sense. Quantum theory tells us that given a single quantum state it is impossible to determine it exactly. One needs an infinite number of identically prepared quantum states (copies) to know a state exactly. This has remarkable consequences in quantum information theory. One is the familiar no-cloning theorem for a single quantum .
Similar to the quantum no-cloning theorem, there is another no-go theorem in quantum information
theory which is called as the no-deleting theorem
. Like the no-cloning theorem this has important implications in quantum computing, quantum information
theory and quantum mechanics
in general.
The process of quantum deleting takes two copies of an arbitrary, unknown
quantum state at the input port and outputs a blank state along with the original. Mathematically,
this can be described by: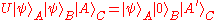
,
where
is the deleting operation which is not necessarily unitary (but a linear operator), 
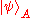is the unknown quantum
state,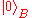
is the blank state, 
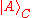is the initial state of
the deleting machine and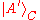
is the final state of the machine.
It may be noted that classical bits can be copied and deleted, as can qubits in orthogonal states. For example, if we have two identical qubits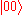
and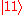 
then we can transform to 
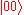and 
. In this case we have deleted the second copy. However, it follows from linearity of quantum theory that there is no 
that can perform the deleting operation for any arbitrary state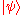 
.
Theorem
Let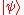
be an unknown quantum state in some Hilbert space (and other states have their usual meaning). Then,
there is no linear isometric transformation such that
, with the final state of the ancilla being independent of
.
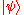let us consider the deleting transformation for two identical qubits. If two qubits are in orthogonal states then we have
,
.
Let
be the state of an unknown qubit. If we have two copies of an unknown qubit, then by linearity of the deleting transformation we have
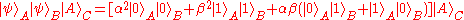
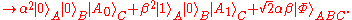
In the above expression, the following transformation has been used: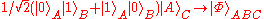
.
However, if we are able to delete a copy, then at the output port of the deleting machine the combined state should be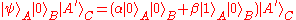
.
In general, these states are not identical and hence we can say that the machine fails to delete a copy. If we require that the final output states are same, then we will see that there is only one
option: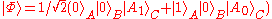
, and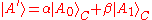
.
Since final state of the ancilla is normalized for all values of
it must be true that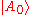
and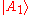 
are orthogonal.
This means that the quantum information is simply in the final state of the ancilla. One can always
obtain the unknown state from the final state of the ancilla using local operation on the ancilla
Hilbert space. Thus, linearity of quantum theory does not allow an unknown quantum state to be deleted
perfectly.
Similar to the quantum no-cloning theorem, there is another no-go theorem in quantum information
theory which is called as the no-deleting theorem
Quantum deleting
Suppose that there are two copies of an unknown quantum state. A pertinent question in this context is to ask if it is possible given two identical copies to delete one of them using quantum mechanical operations? It turns out that we cannot. The no-deleting theorem is a consequence of linearity of quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. Like the no-cloning theorem this has important implications in quantum computing, quantum information
Quantum information
In quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
theory and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
in general.
The process of quantum deleting takes two copies of an arbitrary, unknown
quantum state at the input port and outputs a blank state along with the original. Mathematically,
this can be described by:
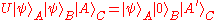,where
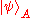is the deleting operation which is not necessarily unitary (but a linear operator), is the unknown quantumstate,
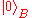is the blank state, 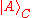is the initial state ofthe deleting machine and
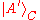is the final state of the machine.It may be noted that classical bits can be copied and deleted, as can qubits in orthogonal states. For example, if we have two identical qubits
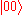and 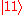then we can transform to 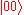and 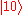. In this case we have deleted the second copy. However, it follows from linearity of quantum theory that there is no that can perform the deleting operation for any arbitrary state 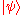.Theorem
Let
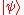be an unknown quantum state in some Hilbert space (and other states have their usual meaning). Then,there is no linear isometric transformation such that
, with the final state of the ancilla being independent of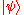.Proof
The theorem holds for quantum states in any Hilbert space dimension. For simplicity,let us consider the deleting transformation for two identical qubits. If two qubits are in orthogonal states then we have
,.Let
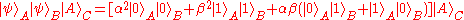
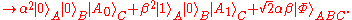
be the state of an unknown qubit. If we have two copies of an unknown qubit, then by linearity of the deleting transformation we haveIn the above expression, the following transformation has been used:
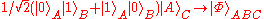.However, if we are able to delete a copy, then at the output port of the deleting machine the combined state should be
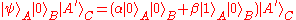.In general, these states are not identical and hence we can say that the machine fails to delete a copy. If we require that the final output states are same, then we will see that there is only one
option:
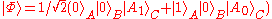, and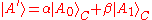.Since final state of the ancilla is normalized for all values of
it must be true that
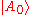and 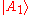are orthogonal.This means that the quantum information is simply in the final state of the ancilla. One can always
obtain the unknown state from the final state of the ancilla using local operation on the ancilla
Hilbert space. Thus, linearity of quantum theory does not allow an unknown quantum state to be deleted
perfectly.
Consequence
- If it were possible to delete an unknown quantum state then using two pairs of EPR states we could send signals faster than light. Thus, the no-deleting theorem is inconsistent with the no-signalling condition.
- The no-cloning and the no-deleting theorems point to conservation of quantum information.
- A stronger version of the no-cloning theorem and the no-deleting theorem provide permanence to quantum information. To create a copy one must import the information from some part of the universe and to delete a state one needs to export it to another part of the universe where it will continue to exist.
See also
- No-broadcast theoremNo-broadcast theoremThe no-broadcast theorem is a result in quantum information theory. In the case of pure quantum states, it is a corollary of the no-cloning theorem: since quantum states cannot be copied in general, they cannot be broadcast...
- No-cloning theorem
- No-hiding theorem
- Quantum teleportationQuantum teleportationQuantum teleportation, or entanglement-assisted teleportation, is a process by which a qubit can be transmitted exactly from one location to another, without the qubit being transmitted through the intervening space...
- Quantum entanglementQuantum entanglementQuantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
- Quantum informationQuantum informationIn quantum mechanics, quantum information is physical information that is held in the "state" of a quantum system. The most popular unit of quantum information is the qubit, a two-level quantum system...
- Uncertainty principleUncertainty principleIn quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
- Quantum cloningQuantum cloningQuantum cloning is the process that takes an arbitrary, unknown quantum state and makes an exact copy without altering the original state in any way...