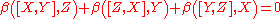Quasi-Frobenius Lie algebra
Encyclopedia
In mathematics
, a quasi-Frobenius Lie algebra
over a field
is a Lie algebra
equipped with a nondegenerate skew-symmetric bilinear form
, which is a Lie algebra 2-cocycle
of
with values in 
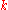. In other words,
for all
, 
, 
in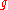 
.
If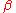
is a coboundary, which means that there exists a linear form 
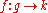such that
then
is called a Frobenius Lie algebra.
is a quasi-Frobenius Lie algebra, one can define on 
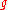another bilinear product 
by the formula
Then one has
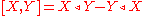and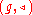
is a pre-Lie algebra
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quasi-Frobenius Lie algebra
over a field
is a Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
equipped with a nondegenerate skew-symmetric bilinear form
, which is a Lie algebra 2-cocycleCocycle
A cocycle refers to any one of the following:*A closed cochain in algebraic topology is called a cocycle.*A particular type of map in an autonomous dynamical system; see Oseledec theorem....
of
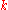with values in . In other words,
for all
, , in 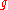.If
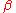is a coboundary, which means that there exists a linear form 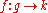such thatthen
is called a Frobenius Lie algebra.
Equivalence with pre-Lie algebras with nondegenerate invariant skew-symmetric bilinear form
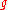If is a quasi-Frobenius Lie algebra, one can define on another bilinear product by the formula
-
.
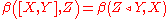Then one has
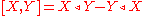and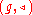is a pre-Lie algebra
Pre-Lie algebra
In mathematics, a pre-Lie algebra is an algebraic structure on a vector space, that describes some properties of objects such as rooted trees and vector fields on affine space....
.
See also
- Lie coalgebraLie coalgebraIn mathematics a Lie coalgebra is the dual structure to a Lie algebra.In finite dimensions, these are dual objects: the dual vector space to a Lie algebra naturally has the structure of a Lie coalgebra, and conversely.-Definition:...
- Lie bialgebraLie bialgebraIn mathematics, a Lie bialgebra is the Lie-theoretic case of a bialgebra: its a set with a Lie algebra and a Lie coalgebra structure which are compatible....
- Lie algebra cohomologyLie algebra cohomologyIn mathematics, Lie algebra cohomology is a cohomology theory for Lie algebras. It was defined by in order to give an algebraic construction of the cohomology of the underlying topological spaces of compact Lie groups...
- Frobenius algebraFrobenius algebraIn mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
- Quasi-Frobenius ringQuasi-Frobenius ringIn ring theory, the class of Frobenius rings and their generalizations are the extension of work done on Frobenius algebras. Perhaps the most important generalization is that of quasi-Frobenius rings , which are in turn generalized by right pseudo-Frobenius rings and right finitely...