
Quasilinear utility
Encyclopedia
In economics
and consumer theory
, quasilinear utility
functions are linear in one argument, generally the numeraire
. This utility function has the representation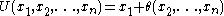 . In two dimensional case, if
. In two dimensional case, if 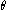 is concave
is concave
, this has the interpretation that the indifference curves are parallel
; which is useful because the entire utility function can be determined from a single indifference curve.
 is quasilinear if (1) if
is quasilinear if (1) if  then
then 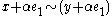 , where
, where 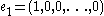 and
and  is a real number. The two definitions are equivalent in the case of a convex
is a real number. The two definitions are equivalent in the case of a convex
consumption set with continuous
preferences that are locally non-satiated in the first argument.
Informally, an agent has quasilinear utility if it can express all its preferences in terms of money and the amount of money it has will not create a wealth effect
. As a practical matter in mechanism design, quasilinear utility ensures that agents can compensate each other with side payments. In regards to surplus, quasilinear preferences entail that Marshallian surplus will equal Hicksian surplus since there would be no wealth effect for a change in price.
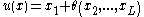 , where
, where 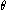 is a function. In the case of two goods, this function could be, for example,
is a function. In the case of two goods, this function could be, for example, 
More formally, the preference relation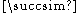 on a set
on a set 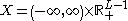 is quasilinear with respect to commodity 1 (called, in this case, the numeraire commodity) if:
is quasilinear with respect to commodity 1 (called, in this case, the numeraire commodity) if:
Suppose F(L,K) = K^2 + L
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
and consumer theory
Consumer theory
Consumer choice is a theory of microeconomics that relates preferences for consumption goods and services to consumption expenditures and ultimately to consumer demand curves. The link between personal preferences, consumption, and the demand curve is one of the most closely studied relations in...
, quasilinear utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
functions are linear in one argument, generally the numeraire
Numéraire
Numéraire is a basic standard by which values are measured. Acting as the numéraire is one of the functions of money, to serve as a unit of account: to measure the worth of different goods and services relative to one another, i.e. in same units...
. This utility function has the representation
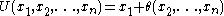 . In two dimensional case, if
. In two dimensional case, if 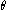 is concave
is concaveConcave
The word concave means curving in or hollowed inward, as opposed to convex. The former may be used in reference to:* Concave lens, a lens with inward-curving surfaces.* Concave polygon, a polygon which is not convex....
, this has the interpretation that the indifference curves are parallel
Parallel
-Mathematics and science:* Parallel , an imaginary east-west line circling a globe* Parallel circuits, as opposed to series* Parallel * Parallel evolution* Parallel transport* Parallel of declination, used in astronomy-Computing:...
; which is useful because the entire utility function can be determined from a single indifference curve.
Definition in terms of preferences
Quasilinearity can also be defined as a property of preferences directly;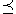 is quasilinear if (1) if
is quasilinear if (1) if 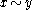 then
then 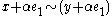 , where
, where 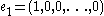 and
and  is a real number. The two definitions are equivalent in the case of a convex
is a real number. The two definitions are equivalent in the case of a convexConvex preferences
In economics, convex preferences refer to a property of an individual's ordering of various outcomes which roughly corresponds to the idea that "averages are better than the extremes"...
consumption set with continuous
Indifference curve
In microeconomic theory, an indifference curve is a graph showing different bundles of goods between which a consumer is indifferent. That is, at each point on the curve, the consumer has no preference for one bundle over another. One can equivalently refer to each point on the indifference curve...
preferences that are locally non-satiated in the first argument.
Informally, an agent has quasilinear utility if it can express all its preferences in terms of money and the amount of money it has will not create a wealth effect
Wealth effect
The wealth effect is an economic term, referring to an increase in spending that accompanies an increase in perceived wealth.-Effect on individuals:...
. As a practical matter in mechanism design, quasilinear utility ensures that agents can compensate each other with side payments. In regards to surplus, quasilinear preferences entail that Marshallian surplus will equal Hicksian surplus since there would be no wealth effect for a change in price.
Quasilinearity in Microeconomics
A preference relation is quasilinear if there is one commodity, called the numeraire, which shifts the indifference curves outward as consumption of it increases, without changing their slope. It is possible to extend this definition to utility functions: a continuous preference relation is quasilinear in commodity 1 if there is a utility function that represents it in the form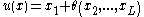 , where
, where 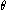 is a function. In the case of two goods, this function could be, for example,
is a function. In the case of two goods, this function could be, for example, 
More formally, the preference relation
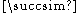 on a set
on a set 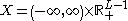 is quasilinear with respect to commodity 1 (called, in this case, the numeraire commodity) if:
is quasilinear with respect to commodity 1 (called, in this case, the numeraire commodity) if:
- All the indifference sets are parallel displacements of each other along the axis of commodity 1. That is, if a bundle "x" is indifferent to a bundle "y" (x~y), then
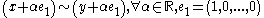
- good 1 is desirable; that is,
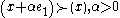
2 common examples
Suppose U(x, v) = ln(x) + v- This function is also quasi-linear; the function is linear in v and non-linear in x
Suppose F(L,K) = K^2 + L
- This is a quasi-linear production function; the function is linear in L and non-linear in K

