
Quasiperiodic function
Encyclopedia
In mathematics
, a function
is said to be quasiperiodic when it has some similarity to a periodic function but does not meet the strict definition.
A simple case (sometimes called arithmetic quasiperiodic) is if the function obeys the equation:
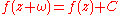
Another case (sometimes called geometric quasiperiodic) is if the function obeys the equation:

A useful example is the function:

If the ratio A/B is rational, this will have a true period, but if A/B is irrational there is no true period, but a succession of increasingly accurate "almost" periods.
A function with quasiperiod (sometimes simply called the period) ω if for certain constants a and b, f satisfies the functional equation
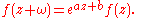
An example of this is the Jacobi theta function, where
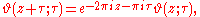
shows that for fixed τ it has quasiperiod τ; it also is periodic with period one. Another example is provided by the Weierstrass sigma function
, which is quasiperiodic in two independent quasiperiods, the periods of the corresponding Weierstrass ℘ function.
Functions with an additive functional equation
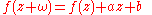
are also called quasiperiodic. An example of this is the Weierstrass zeta function, where

for a fixed constant η when ω is a period of the corresponding Weierstrass ℘ function.
In the special case where we say f is periodic
we say f is periodic
with period ω.
s and that article should be consulted. The more vague and general notion of quasiperiodicity
has even less to do with quasiperiodic functions in the mathematical sense.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is said to be quasiperiodic when it has some similarity to a periodic function but does not meet the strict definition.
A simple case (sometimes called arithmetic quasiperiodic) is if the function obeys the equation:
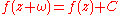
Another case (sometimes called geometric quasiperiodic) is if the function obeys the equation:

A useful example is the function:

If the ratio A/B is rational, this will have a true period, but if A/B is irrational there is no true period, but a succession of increasingly accurate "almost" periods.
A function with quasiperiod (sometimes simply called the period) ω if for certain constants a and b, f satisfies the functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
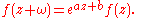
An example of this is the Jacobi theta function, where
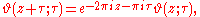
shows that for fixed τ it has quasiperiod τ; it also is periodic with period one. Another example is provided by the Weierstrass sigma function
Weierstrass sigma function
In mathematics, the Weierstrass functions are special functions of a complex variable that are auxiliary to the Weierstrass elliptic function. They are named for Karl Weierstrass.-Weierstrass sigma-function:...
, which is quasiperiodic in two independent quasiperiods, the periods of the corresponding Weierstrass ℘ function.
Functions with an additive functional equation
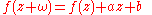
are also called quasiperiodic. An example of this is the Weierstrass zeta function, where

for a fixed constant η when ω is a period of the corresponding Weierstrass ℘ function.
In the special case where
 we say f is periodic
we say f is periodicPeriodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
with period ω.
Quasiperiodic signals
Quasiperiodic signals in the sense of audio processing are not quasiperiodic functions; instead they have the nature of almost periodic functionAlmost periodic function
In mathematics, an almost periodic function is, loosely speaking, a function of a real number that is periodic to within any desired level of accuracy, given suitably long, well-distributed "almost-periods". The concept was first studied by Harald Bohr and later generalized by Vyacheslav Stepanov,...
s and that article should be consulted. The more vague and general notion of quasiperiodicity
Quasiperiodicity
Quasiperiodicity is the property of a system that displays irregular periodicity. Periodic behavior is defined as recurring at regular intervals, such as "every 24 hours". Quasiperiodic behavior is a pattern of recurrence with a component of unpredictability that does not lend itself to precise...
has even less to do with quasiperiodic functions in the mathematical sense.
External links
- Quasiperiodic function at PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...

