Quasiregular element
Encyclopedia
In mathematics
, specifically ring theory
, the notion of quasiregularity provides a computationally convenient way to work with the Jacobson radical
of a ring. Intuitively, quasiregularity captures what it means for an element of a ring to be "bad"; that is, have undesirable properties. Although a "bad element" is necessarily quasiregular, quasiregular elements need not be "bad," in a rather vague sense. In this article, we primarily concern ourselves with the notion of quasiregularity for unital rings. However, one section is devoted to the theory of quasiregularity in non-unital rings, which constitutes an important aspect of noncommutative ring theory.
in R; that is, invertible under multiplication. The notions of right or left quasiregularity correspond to the situations where 1 - r has a right or left inverse, respectively.
An element x of a non-unital ring is said to be right quasiregular if there is y such that
. The notion of a left quasiregular element is defined in an analogous manner. The element y is sometimes referred to as a right quasi-inverse of x. If the ring is unital, this definition quasiregularity coincides with that given above. If one writes 
, then this binary operation 
is associative. Therefore, if an element possesses both a left and right quasi-inverse, they are equal.
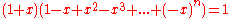
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, the notion of quasiregularity provides a computationally convenient way to work with the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
of a ring. Intuitively, quasiregularity captures what it means for an element of a ring to be "bad"; that is, have undesirable properties. Although a "bad element" is necessarily quasiregular, quasiregular elements need not be "bad," in a rather vague sense. In this article, we primarily concern ourselves with the notion of quasiregularity for unital rings. However, one section is devoted to the theory of quasiregularity in non-unital rings, which constitutes an important aspect of noncommutative ring theory.
Definition
Let R be a ring (with unity) and let r be an element of R. Then r is said to be quasiregular, if 1 - r is a unitUnit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in R; that is, invertible under multiplication. The notions of right or left quasiregularity correspond to the situations where 1 - r has a right or left inverse, respectively.
An element x of a non-unital ring is said to be right quasiregular if there is y such that
. The notion of a left quasiregular element is defined in an analogous manner. The element y is sometimes referred to as a right quasi-inverse of x. If the ring is unital, this definition quasiregularity coincides with that given above. If one writes , then this binary operation is associative. Therefore, if an element possesses both a left and right quasi-inverse, they are equal.Examples
- If R is a ring, then the additive identity of R is always quasiregular
- If
is right (resp. left) quasiregular, then 
is right (resp. left) quasiregular. - If R is a ring, every nilpotent element of R is quasiregular. This fact is also supported by an elementary computation:
- If
, then
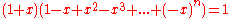
- A matrix is quasiregular in a matrix ringMatrix ringIn abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
if it does not possess -1 as an eigenvalue. More generally, a bounded operatorBounded operatorIn functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
is quasiregular if -1 is not in its spectrum. - In a unital Banach algebra, if
, then the geometric series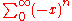 
converges. Consequently, every such x is quasiregular. - If R is a ring and S=RX1,...,Xn denotes the ring of formal power seriesFormal power seriesIn mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
in n intederminants over R, an element of S is quasiregular if and only its constant term is quasiregular as an element of R.
Properties
- Every element of the Jacobson radicalJacobson radicalIn mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
of a (not necessarily commutative) ring is quasiregular. In fact, the Jacobson radical of a ring can be characterized as the unique right ideal of the ring, maximal with respect to the property that every element is right quasiregular. However, a right quasiregular element need not necessarily be a member of the Jacobson radical. This justifies the remark in the beginning of the article - "bad elements" are quasiregular, although quasiregular elements are not necessarily "bad." Elements of the Jacobson radical of a ring, are often deemed to be "bad."
- If an element of a ring is nilpotent and central, then it is a member of the ring's Jacobson radical. This is because the principal right idealPrincipal idealIn ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
generated by that element consists of quasiregular (in fact, nilpotent) elements only.
- If an element, r, of a ring is idempotent, it cannot be a member of the ring's Jacobson radical. This is because idempotent elements cannot be quasiregular. This property, as well as the one above, justify the remark given at the top of the article that the notion of quasiregularity is computationally convenient when working with the Jacobson radical.
See also
- Jacobson radicalJacobson radicalIn mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
- NilradicalNilradicalIn algebra, the nilradical of a commutative ring is the ideal consisting of the nilpotent elements of the ring. In the non-commutative ring case, more care is needed resulting in several related radicals.- Commutative rings :...
- Unit (ring theory)Unit (ring theory)In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
- Nilpotent element
- Center of a ring
- Idempotent element