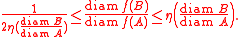Quasisymmetric map
Encyclopedia
In mathematics
, a quasisymmetric homeomorphism
between metric spaces is a map that generalizes bi-Lipschitz maps. While bi-Lipschitz maps shrink or expand the diameter of a set by no more than a multiplicative factor, quasisymmetric maps satisfy the weaker geometric property that they preserve the relative sizes of sets: if two sets A and B have diameters t and are no more than distance t apart, then the ratio of their sizes changes by no more than a multiplicative constant. These maps are also related to quasiconformal maps, since in many circumstances they are in fact equivalent.
s. A homeomorphism
f:X → Y is said to be η-quasisymmetric if there is an increasing function η : [0, ∞) → [0, ∞) such that for any triple x, y, z of distinct points in X, we have
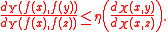
Quasisymmetric maps preserve relative sizes of sets : If A and B are subsets of X and A is a subset of B, then

Not all weakly quasisymmetric maps are quasisymmetric. However, if X is connected
and doubling, then all weakly quasisymmetric maps are quasisymmetric. The appeal of this result is that proving weak-quasisymmetry is much easier than proving quasisymmetry directly, and in many natural settings we have the luck of knowing the two are equivalent.
H is δ-monotone if for all x and y in H,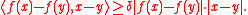
To grasp what this condition means geometrically, suppose f(0) = 0 and consider the above estimate when y = 0. Then it implies that the angle between the vector x and its image f(x) stays between 0 and arccos δ < π/2.
These maps are quasisymmetric, although they are a much narrower subclass of quasisymmetric maps. For example, while a general quasisymmetric map in the complex plane could map the real line to a set of Hausdorff dimension
strictly greater than one, a δ-monotone will always map the real line to a rotated graph
of a Lipschitz function L:ℝ → ℝ.
to itself can be characterized in terms of their derivatives. An increasing homeomorphism f:ℝ → ℝ is quasisymmetric if and only if there is a constant C > 0 and a doubling measure μ on the real line such that


Writing it this way, we can attempt to define a map using this same integral, but instead integrate (what is now a vector valued integrand) over ℝn: if μ is a doubling measure on ℝn and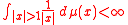
then the map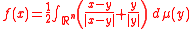
is quasisymmetric (in fact, it is δ-monotone for some δ depending on the measure μ).
Conversely, if f : Ω → Ω´ is K-quasiconformal and B(x, 2r) is contained in Ω, then f is η-quasisymmetric on B(x, r), where η depends only on K.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a quasisymmetric homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
between metric spaces is a map that generalizes bi-Lipschitz maps. While bi-Lipschitz maps shrink or expand the diameter of a set by no more than a multiplicative factor, quasisymmetric maps satisfy the weaker geometric property that they preserve the relative sizes of sets: if two sets A and B have diameters t and are no more than distance t apart, then the ratio of their sizes changes by no more than a multiplicative constant. These maps are also related to quasiconformal maps, since in many circumstances they are in fact equivalent.
Definition
Let (X, dX) and (Y, dY) be two metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. A homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
f:X → Y is said to be η-quasisymmetric if there is an increasing function η : [0, ∞) → [0, ∞) such that for any triple x, y, z of distinct points in X, we have
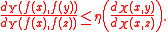
Basic properties
Inverses are quasisymmetric : If f : X → Y is an invertible η-quasisymmetric map as above, then its inverse map is ή-quasisymmetric, where ή(t) = 1/η(1/t).Quasisymmetric maps preserve relative sizes of sets : If A and B are subsets of X and A is a subset of B, then
Weakly quasisymmetric maps
A map f:X→Y is said to be H-weakly-quasisymmetric for some H > 0 if for all triples of distinct points x,y,z in X, we have
Not all weakly quasisymmetric maps are quasisymmetric. However, if X is connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
and doubling, then all weakly quasisymmetric maps are quasisymmetric. The appeal of this result is that proving weak-quasisymmetry is much easier than proving quasisymmetry directly, and in many natural settings we have the luck of knowing the two are equivalent.
δ-monotone maps
A monotone map f:H → H on a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H is δ-monotone if for all x and y in H,
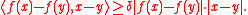
To grasp what this condition means geometrically, suppose f(0) = 0 and consider the above estimate when y = 0. Then it implies that the angle between the vector x and its image f(x) stays between 0 and arccos δ < π/2.
These maps are quasisymmetric, although they are a much narrower subclass of quasisymmetric maps. For example, while a general quasisymmetric map in the complex plane could map the real line to a set of Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
strictly greater than one, a δ-monotone will always map the real line to a rotated graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of a Lipschitz function L:ℝ → ℝ.
The real line
Quasisymmetric homeomorphisms of the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
to itself can be characterized in terms of their derivatives. An increasing homeomorphism f:ℝ → ℝ is quasisymmetric if and only if there is a constant C > 0 and a doubling measure μ on the real line such that

Euclidean space
An analogous result holds in Euclidean space. Suppose C = 0 and we rewrite the above equation for f as
Writing it this way, we can attempt to define a map using this same integral, but instead integrate (what is now a vector valued integrand) over ℝn: if μ is a doubling measure on ℝn and
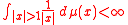
then the map
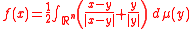
is quasisymmetric (in fact, it is δ-monotone for some δ depending on the measure μ).
Quasisymmetry and quasiconformality in Euclidean space
Let Ω and Ω´ be open subsets of ℝn. If f : Ω → Ω´ is η-quasisymmetric, then it is also K-quasiconformal, where K > 0 is a constant depending on η.Conversely, if f : Ω → Ω´ is K-quasiconformal and B(x, 2r) is contained in Ω, then f is η-quasisymmetric on B(x, r), where η depends only on K.